Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 6.Exercícios Propostos - Ex. 6

Dados os pontos A = 1,2 , 3   e   B = 0 , 1 , 2 e ainda os pontos C = ( - 1,0 , 1 ) , D = 1 2 , 3 2 , 5 2   e   E = ( 2,3 , 4 ) . (a) Escreva equações da reta A B ; (b) verifique quais dos pontos C , D   e   E estão na reta A B ;   (c) situe esses pontos na reta

Passo 1

Fala ae, galera! Blz? 😊

Para escrevermos a equação da reta A B precisamos do seu vetor diretor e de um ponto que pertence a essa reta.

Passo 2

Letra a):

O vetor diretor da reta é A B → . Assim:

A B → = B - A = - 1 , - 1 , - 1

O ponto A = ( 1,2 , 3 ) é um ponto pertencente a reta, logo a equação paramétrica da reta é:

r : x = 1 - t y = 2 - t z = 3 - t ; t ∈ R

Passo 3

Letra b):

Os pontos C ,   D e E estão na reta se satisfazem a equação da reta. Portanto:

C = ( - 1,0 , 1 )   ∈ r ?

r : - 1 = 1 - t 0 = 2 - t 1 = 3 - t ; t ∈   R

L 2 : t = 2

L 3 : - t = - 2 → t = 2

L 1 : - t = - 2 → t = 2

Portanto, C = ( - 1,0 , 1 )   ∈ r .

Passo 4

D = ( 1 2 , 3 2 , 5 2 )   ∈ r ?

r : 1 2 = 1 - t 3 2 = 2 - t 5 2 = 3 - t ; t ∈   R

L 1 : t = 1 2

L 2 : t = 1 2

L 3 : t = 1 2

Portanto, D = 1 2 , 3 2 , 5 2 ∈ r .

Passo 5

E = ( 2 , 3 , 4 )   ∈ r ?

r : 2 = 1 - t 3 = 2 - t 4 = 3 - t ; t ∈   R

L 1 : t = - 1

L 2 : t = - 1

L 3 : t = - 1

Portanto, E = 2,3 , 4 ∈ r .

Passo 6

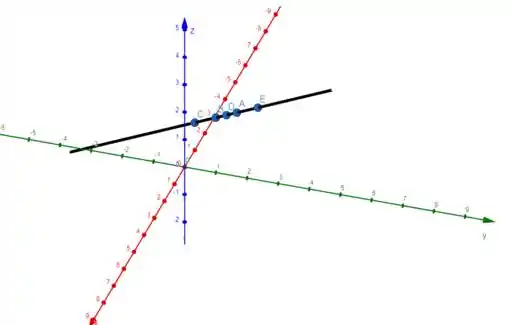
Letra c): Posicionando os pontos na reta e montando seu gráfico, temos:

Resposta

a :   r : x = 1 - t y = 2 - t z = 3 - t ; t ∈ R

b : C ,   D   e   E   p e r t e n c e m   a   r e t a .

c :

Exercícios de Livros Relacionados

Achar a distancia do ponto P à reta r nos casos P 1 , - 1 , 0 r : x = 2 - t y = 0 z = t
Achar a distancia do ponto P à reta r nos casos P 3,2 , 1 r : y = 2 x z = x + 3
Calcule a distância do ponto P à reta r .c) P = 1 , - 1,4 , r : x - 2 4 = y - 3 = 1 - z 2
Determine as coordenadas do simétrico ao ponto P = ( 2 , - 3 ) em relação a:a.Ao eixo OX;b.Ao eixo OY;c.À diagonal ∆ d.Ao ponto (-3,2).
Mostre que a equação da tangente à circunferência A x 2 + A y 2 + D x + E y + F = 0 no ponto x 1 , y 1éa x - x 1 + b y - y 1 = 0 é , onde a = x 1 + D 2 Aeb = x 2 + E 2 A