Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 13.Problemas - Ex. 1

Mostre que a equação da tangente à circunferência A x 2 + A y 2 + D x + E y + F = 0 no ponto x 1 , y 1   é   a x - x 1 + b y - y 1 = 0 , onde a = x 1 + D 2 A   e   b = x 2 + E 2 A

Passo 1

Falaaa, beleza? Para começar essa questão vamos tomar uma primeira atitude pensando no que ele pede.

Veja que ele define a e b como algo sobre 2A, além disso os valores de x e y estão sem nada multiplicando eles, então vamos dividir toda equação da circunferência por A para aparecer algo mais parecido:

C :         x 2 + y 2 + D A x + E A y + F A = 0

Agora vamos completar quadrado:

x + D 2 A 2 - D 2 4 A 2 + y + E 2 A 2 - E 2 4 A 2 + F A = 0

x + D 2 A 2 + y + E 2 A 2 = D 2 + E 2 - 4 A F 4 A 2

Passo 2

Ou seja, temos que o centro da nossa circunferência é - D 2 A , - E 2 A

Agora vamos usar um desenho para nos ajudar a ter uma ideia:

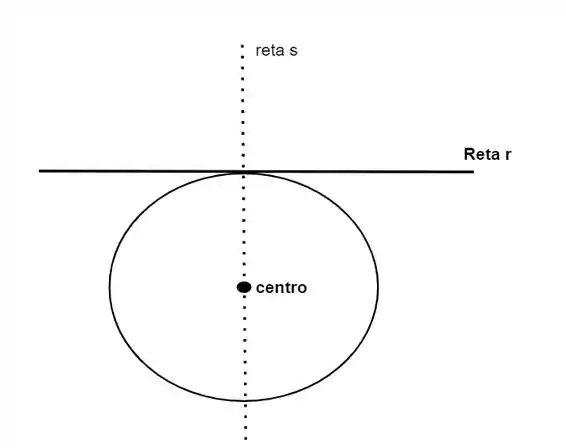
Temos que r é a reta tangente que estamos estudando e a reta s a reta que passa pelo centro e pelo ponto de tangencia e ambas são perpendiculares

Vamos achar qual a equação da reta s, usando que passa pelo centro e pelo ponto ( x 1 , y 1 )

Passo 3

Inclinação da reta s:

m = y 1 + E 2 A x 1 + D 2 A

Como as retas r e s são perpendiculares, temos que se multiplicarmos os coeficientes angulares das 2 o resultado é -1.

m r   ∙ m =   - 1

m r =   - 1 y 1 + E 2 A x 1 + D 2 A

Agora sabemos que a equação da reta é:

y - y 1 = m r ( x - x 1 )

y - y 1 - m r x - x 1 = 0

Substituindo:

y - y 1 + 1 y 1 + E 2 A x 1 + D 2 A x - x 1 = 0

Multiplicando tudo por y 1 + E 2 A :

y - y 1 y 1 + E 2 A + x 1 + D 2 A x - x 1 = 0

Exatamente o que queríamos.

Resposta

Demonstração

Exercícios de Livros Relacionados

Determine a distância ∆ do ponto P = 3,1 à reta x + 2 y = 3 . Ache o ponto Q = x , y sobre esta reta, tal que d P , Q = ∆ .
Escreva a equação da circunferência que tem centro no ponto P = (2, 5) e é tangente à reta y = 3x + 1.
Sabendo que x = cos t, y = sin t, t ∈ [0, 2π], são equações paramétricas da circunferência x²+y²=1, obter equações paramétricas para a circunferência de centro P = (a, b) e raio r.
Mostre que a reta y = ax + b é tangente à circunferência x² + y² = r² se, e somente se, b² = (1 + a²)r².
Esboce o conjunto dos pontos do plano cujas coordenadas satisfazem a equaçãox³ + xy² − x – x²y – y³ + y = 0.