Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 10b
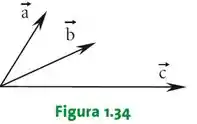
Dados os vetores , e (Figura 1.34), apresentar graficamente um representante do vetor tal que
b)
Passo 1
Vamos isolar o vetor , vamos achar que
Passo 2
Fazer a soma de :
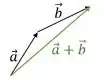
Passo 3
Agora vamos pegar esse vetor que vem da soma que fizemos de e somar com o vetor para acharmos a equação , fica assim:
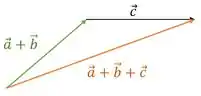
Passo 4
Como , vamos inverter o sentido do vetor que encontramos:
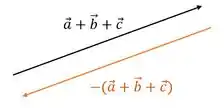
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Sejam A, B, C e D vértices de um quadrado, E um ponto de AD e F um ponto de CD, tais que o triângulo CEF seja equilátero. Calcule a razão em que E divide (A,D) e a razão em que F divide (D,C).
Sejam s 1 e t 1 duas retas concorrentes em B, tangentes à circunferência de centro A e raio r 1 , (Figura 5-10). Com centro em um ponto P da semi-reta de origem B que contém A, traça-se a circunferênc
(b) Sejam OABC um tetraedro e X o baricentro do triângulo ABC. Exprima O X → em função de O A → , O B → e O C → .
Dado o triângulo ABC não retângulo, a = t g ,  b = t gB ^ e c = t gC ^ .Sendo CX a altura relativa ao vértice C, prove que a A X → = b X B → e exprima C X → em função de C A → ,C B → ,a ,b .
Dado o triângulo ABC, seja X a interseção do lado AB com a bissetriz do ângulo interno de vértice C (Figura 5-8) e sejam a = | | C B → | | e b = | | C A → | | .Explique geometricamente por que C X → é