Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 10a
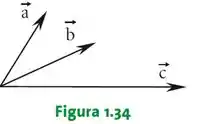
Dados os vetores , e (Figura 1.34), apresentar graficamente um representante do vetor tal que
Passo 1
Como já temos o vetor isolado, vamos achar quem são os vetores , e
O vetor tem mesma direção e sentido do vetor , só que com 4 vezes o tamanho de , graficamente ele fica assim:
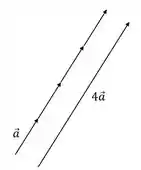
Já o vetor tem o dobro do tamanho de , mas com sentido oposto ao vetor da figura, então temos:
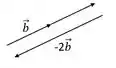
E o vetor é o vetor com sentido contrário, ou seja:
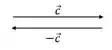
Passo 2
Vamos fazer primeiro a soma de :
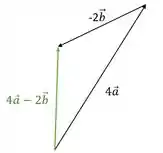
Passo 3
Agora vamos pegar esse vetor que vem da soma que fizemos de e somar com o vetor para acharmos a equação , que é o que o enunciado pede:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Prove que o segmento que une os pontos médios dos lados não-paralelos de um trapézio é paralelo às bases, e sua medida é a média aritmética das medidas das bases.
10. Utilize o paralelepípedo da figura 2-9 (a) para determinar o vetor x → em cada caso:a) x → = G H → - H E → - F E → + A E → + A B → b) x → = H D → - C F → + D G → + B C → + A F → - B E → c) x → = A
(a) No triângulo ABC da Figura 5-2 (a), M divide (A,B) e N divide (C,B) na mesma razão r. Prove MN//AC e calcule M N → | A C → | .
Dado o triângulo ABC, tome D na reta BC tal que C seja o ponto médio de BD e Y na reta AC tal que as retas AD e BY sejam paralelas. Exprima A Y → em função de B A → ,B C → e mostre que C é o ponto méd
(c) Suponha que o quadrilátero ABCD do item anterior seja um paralelogramo. Mostre que as quatro diagonais (as duas de ABCD e as duas de MNPQ) têm um ponto comum.