Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 23
Sejam A, B, C e D vértices de um quadrado, E um ponto de AD e F um ponto de CD, tais que o triângulo CEF seja equilátero. Calcule a razão em que E divide (A,D) e a razão em que F divide (D,C).
Passo 1
Bora lá!
A questão pede para que calculemos a razão em que E divide (A,D) e a razão em que F divide (D,C). Como o triângulo pedido é equilátero, ele deve ser necessariamente simétrico em relação à diagonal BD do quadrado. Assim, podemos deduzir alguns ângulos:
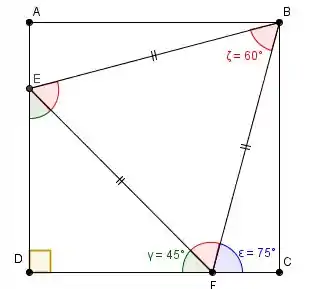
Passo 2
Primeiro, vamos descobrir o módulo de em relação ao lado BC:
Passo 3
Agora, é preciso achar o módulo do vetor e então calcular a proporção gerada por F:
Notem, que como se trar de um quadrado, temos a seguinte equivalência entre os lados:
Passo 4
Utilizando os módulos dos lados e o valor de que achamos no passo 2, podemos calcular o módulo de apenas em função dos lados, vejamos:
Passo 5
Fazendo a divisão entre os módulos dos vetores que compõem o lado, temos:
Analogamente no lado , podemos ver que:
Resposta
Portanto, podemos concluir que a razão em que E divide (A,D) e F divide (D,C) é: