Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 9b
(b) Sejam OABC um tetraedro e X o baricentro do triângulo ABC. Exprima em função de , e
Passo 1
Bora lá!
Primeiro, vamos fazer um esboço do nosso tetraedro
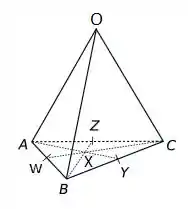
Onde:
- W é o ponto médio do segmento AB;
- Y é o ponto médio do segmento BC e
- Z é o ponto médio do segmento AC.
Passo 2
Solução 1
O modo mais rápido de resolução é aplicando o teorema que diz que a soma dos vetores que representam as medianas de um triângulo é NULA! As faces de um tetraedro são triângulos equiláteros e num triângulo equilátero, as medianas têm o mesmo comprimento.
Somando as equações:
Putz... mas eu nunca nem ouvi falar desse teorema ☹. Relaxa, vamos fazer de um outro jeito.
É um jeito mais demorado e complexo, mas é mais raiz. Vamos lá!
Passo 3
Solução 2
Do nosso tetraedo, temos
Como e , interessa saber qual o valor de . Usando a propriedade do vetor somado ao ponto, as relações anteriores podem ser reescritas da seguinte forma
Mas , logo
Passo 4
Reescrevendo em termos de e , temos
Passo 5
Resolvendo o sisteminha, chegamos em . Então