Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 1.Problemas Propostos - Ex. 2a
Dados os vetores , e como na figura, apresentar um representante de cada um dos vetores:
Passo 1
Vamos primeiro desenhar os vetores , e
Passo 2
Vamos agora desenhar os vetores e
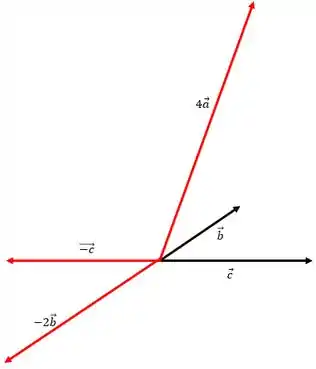
Passo 3
Vamos usar colocar o início de um vetor na extremidade do outro
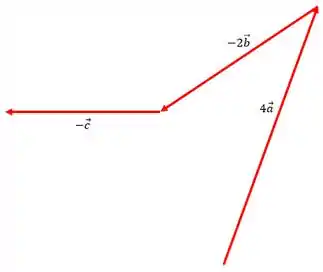
Passo 4
Agora, vamos traçar um vetor do início do vetor até o fim dos nossos vetores enfileirados
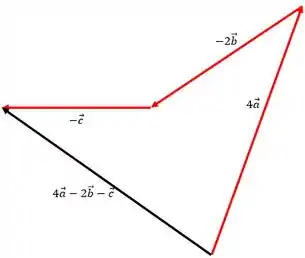
Resposta
Exercícios de Livros Relacionados
Dado o triângulo ABC não retângulo, a = t g ,  b = t gB ^ e c = t gC ^ .Prove que no ortocentro é interior ao triângulo se, e somente se, ele for acutângulo. (No caso em que o triângulo é retângulo,
Dado o triângulo ABC, seja X a interseção do lado AB com a bissetriz do ângulo interno de vértice C (Figura 5-8) e sejam a = | | C B → | | e b = | | C A → | | .Mostre que X divide (A, B) na razão b a
Dado o triângulo da Figura 5-8, sejam a = | | C B → | | e b = | | C A → | | suponhamos que a ≠ b . Seja Y a intersecção da reta AB com a bissetriz do ângulo externo do vértice C.b) Exprima C Y → em fu
Sejam A, B e C vértices de um triângulo.Prove que, se m + n ≠ 0 , então existe um ponto x na reta AB tal que C X → seja paralelo a m C A → + n C B → . Exprima C X → em função de C A → , C B → ,m ,n .
Dado o triângulo ABC não retângulo, a = t g ,  b = t gB ^ e c = t gC ^ .Sendo AY a altura relativa ao vértice A e BZ a altura relativa ao vértice B, exprima A Y → em função de C A → ,C B → ,a ,c e B