Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 2k
Decidir se é verdadeira ou falsa cada uma das afirmações:
Se , o versor de é .
Passo 1
Vamos lá, temos que para cada vetor , , é possível associar dois vetores unitários de mesma direção de : e .
O vetor , que tem o mesmo sentido de , é chamado versor de . Na verdade, o vetor não
é versor só de , mas de todos os vetores paralelos e de mesmo sentido de e medidos com a mesma unidade.
Assim temos na figura abaixo o vetor e o versor :
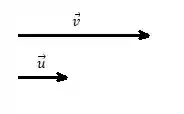
Então temos que o versor é:
Passo 2
Agora vamos achar o versor em comparação a :
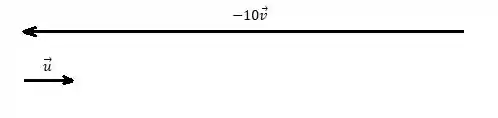
Já aqui temos que:
Pois o vetor está em sentido contrário ao versor, e como foi dito lá no começo, o vetor não é versor só de , mas sim de todos os vetores paralelos e de mesmo sentido de e medidos com a mesma unidade. Assim a afirmação é verdadeira!
Resposta
A afirmação é verdadeira