Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.2 - Ex. 11
Defina a matriz aleatória . Encontre os valores de tais que o sistema homogêneo tem solução não-trivial e para estes valores de , encontre uma base para o espaço solução.
Passo 1
Oiii, tudo certinho?
Se você utilizar o comando no matlab online (que é de graça, se interessar dá uma olhadinha!), você vai obter uma matriz que segue as seguintes propriedades:
Em que é o maior valor que os elementos aleatórios na matriz podem obter, em nosso caso, é 4. E temos uma matriz que é , e outra propriedade da matriz é obtida é que apenas termos da diagonal para cima são diferentes de zero. A que eu obti é da seguinte forma:
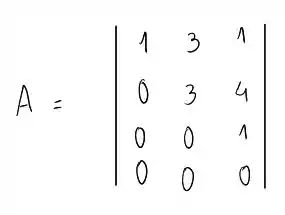
Note no entanto, que é impossível construir uma matriz da forma , já que é a identidade em 4 dimensões, e portanto, é uma matriz . Então qual é o problema aqui? Baseado em spoilers, ou seja, na resposta dada no final do livro, é indicado que na verdade ele queria que esta matriz fosse originalmente , talvez por uma atualização no matlab, matrizes neste formato são obtidas agora utilizando o código , neste processo, obti uma matriz tal que:
Vamos utilizar esta para resolver o nosso problema! Belezinha?
Passo 2
Primeiramente, precisamos escrever a matriz , tal que:
Encontrar os valores de é um problema de autovalores da matriz, portanto, teremos que escrever um polinômio característicos calculando o determinantes desta matriz e ver quando isso é igual a , belezinha? Já que esta é a solução não trivial para a relação . Bora lá!
Passo 3
Mas e agora? Como calcular o determinante desta matriz? Existem métodos analíticos para isso, mas como este é um livro básico de geometria analítica, não é de interesse ir a fundo neles (Você vai ter tempo para aprender isso) Utilizando o matlab, ou qualquer software que você preferir, temos que o determinante é tal que:
Para que tenhamos uma solução não-trivial, é preciso que:
Agora temos um polinômio de quarto grau para achar as raízes, vamos continuar botando o computador para trabalhar, no entanto, existem métodos analíticos que pode utilizar, por exemplo, Briot Ruffini se conseguir achar pelo menos 2 raízes, uma para reduzir à um polinômio de terceiro grau, e a segunda para reduzir à um polinômio de segundo grau. Mas, para este problema, o computador é o suficiente!
Passo 4
O valor que obtive para as raízes é:
O que faz sentido tendo em vista o formato de nossa matriz. Como temos que a parte sob a diagonal é totalmente nula, era possível adivinhar os valores que anulariam a diagonal, e portanto o determinante. Muito bem! Estes são os valores que garantem a nossa solução não-trivial! Obter a base para o espaço de solução é agora um problema de auto-vetores, bora lá!
Passo 5
Encontrar autovetores é encontrar um vetor que obedeça a relação:
Ou seja, para cada autovalor diferente, temos um sistema de quatro equações para os parâmetros (Aiai…). Vamos começar!
Passo 6
Utilizando , temos:
Realizando o produto matricial do lado esquerdo, temos o seguinte sistema de equações:
Como a nossa equação (4) é trivial, temos que apenas 3 equações nos dão informações relevantes, sendo assim, precisamos escolher um parâmetro livre para estabelecer os outros, já que (4) é trivial, vou escolher , beleza?
Sendo assim, temos que de (3):
e de (2) temos:
E nós temos que este sistema independe do valor de , portanto ele pode tomar qualquer valor de forma que nosso vetor pode ser escrito da forma:
ou seja, nosso vetor pode ser escrito em termos de dois geradores e que são L.I. e portanto são base do sistema. Vamos partir para outro autovalor agora, beleza?
Passo 7
Analogamente, temos a equação matricial:
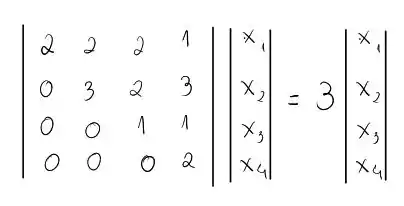
o que nos dá o seguinte sistema de equações:
Esse sistema nos garante que são nulos devido às equações (3) e (4), no entanto, devido a essa informação a equação (2) é trivial. Ou seja, temos que definir um parâmetro livre. Vamos tomar , e assim da equação (1), temos:
Ou seja, nosso vetor tem a forma . Ou seja o vetor é base do nosso espaço solução! Vamos para o último autovalor diferente!
Passo 8
Novamente, temos agora a equação matricial:
Que é equivalente ao sistema:
A equação (3) e (4) nos dão a mesma informação , portanto, temos uma equação a menos para os outros 3 parâmetros, ou seja, novamente, temos que deixar um deles livre. Vamos escolher , o que faz com que tenhamos da equação (2) que:
e da equação (1) que:
e nosso vetor toma a forma . Ou seja, nosso vetor de base é . A questão foi isso, te vejo na próxima! Tchauzinho!