Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 7.Exercício - Ex. 16
Sejam um tetraedro e o ponto médio de . Explique por que é base e determine as coordenadas de nessa base.
Passo 1
Em um exercício assim, o primeiro passo é visualizar e desenhar o tetraedro:
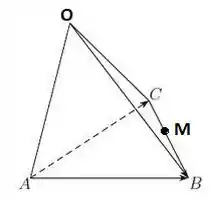
Justificar porque é base é simples: os três vetores não estão no mesmo plano, de modo que são LI. Três vetores LI sempre formam uma base!
Passo 2
O vetor pode ser escrito como
Na última passagem usei que
Por outro lado,
Assim,
Desta forma, temos que
Resposta
Exercícios de Livros Relacionados
Determinar uma base do subespaço do I R 4 gerado pelos vetores v 1 = 1 , - 1,0 , 0 ,v 2 = - 2,2 , 2,1 ,v 3 = - 1,1 , 2,1 ,ev 4 = ( 0,0 , 4,2 ) .
Mostrar que os polinômios p 1 = 1 + 2 x - 3 x 2 ,p 2 = 1 - 3 x + 2 x 2ep 3 = 2 - x + 5 x 2 formam uma base do espaço dos polinômios de grau ≤ 2 e calcular o vetor-coordenada de p = - 2 - 9 x - 13 x 2
Mostrar que o conjunto { 1,1 , 0,0 , 0,0 , 1,1 ,1,0 , 0,3 ,0,0 , 0,5 } é uma base de I R 4 .
Seja V = I R 3 e o conjunto B = 0,1 , 1 ,1,1 , 0 , 1,2 , 1⊂ I R 3 Mostrar que B não é base do I R 3 .Determinar uma base do I R 3 que possua dois elementos de B .
Mostrar que o conjunto 2 3 - 1 0 ,1 - 1 0 - 2 , - 3 - 2 1 - 1 , 3 - 7 - 2 5 é uma base de M 2,2 .