Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 3.Problemas Propostos - Ex. 66
Demonstrar que o segmento cujos extremos são os pontos médios de dois lados de um triângulo é paralelo ao terceiro lado e igual à sua metade.
Passo 1
Devemos demonstrar que segmento cujos extremos são os pontos médios de dois lados de um triângulo é paralelo ao terceiro lado e igual à sua metade. WHAT???
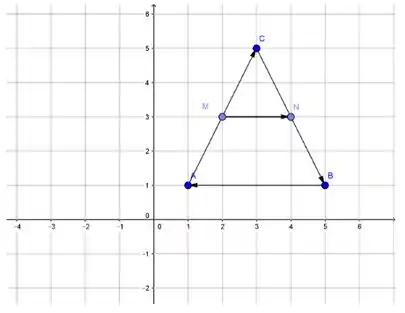
Vamos fazer uma ilustração da situação geométrica proposta para nos ajudar. Para isso, vamos fazer um simples triângulo de vértices , onde representa o ponto médio do lado e o ponto médio do lado :
Beleza, e agora?
Vamos traduzir o nosso enunciado. Em outras palavras, ele quer que nós demonstremos que é paralelo a e que .
Passo 2
Portanto, analisando a ilustração, podemos tirar as seguintes conclusões:
Então:
Portando, .
Passo 3
Por fim, sabemos que dois vetores são paralelos se um é múltiplo do outro, certo?
Temos que:
Então, como onde , podemos concluir que eles paralelos. 😉
Resposta
Ei, a resposta está no passo a passo :)