Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 3.1 - Ex. 15

Demonstre que o segmento que une os pontos médios dos lados não paralelos de um trapézio é paralelo às bases, e sua medida é a média aritmética das medidas das bases. (Sugestão: Mostre que M N → = 1 2 A B → + D C → e depois conclua que M N → é um múltiplo escalar de A B → . Revise o Exemplo 3.3 na página 152).

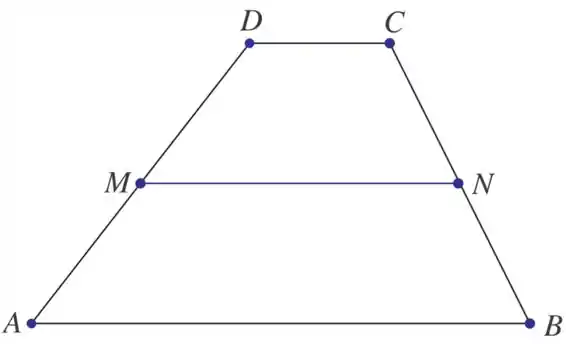
Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de geometria analítica.

Para responder ao questionamento do enunciado, usamos o exemplo citado como suporte:

M N → = M D → + D C → + C N →

Como M é o ponto médio de AD e N é o ponto médio de BC temos que:

M D → = 1 2 A D →   e   C N → = 1 2 C B →

Logo, temos que:

M N → = 1 2 A D → + D C → + 1 2 C B → = 1 2 A D → + 1 2 D C → + 1 2 D C → + 1 2 C B →

M N → = 1 2 A D → + D C → + C B → + 1 2 D C → = 1 2 A B → + D C →

Logo, temos que M N → é um múltiplo escalar de A B → .

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Mostre que se os vetores u e v têm o mesmo comprimento então u + v e u – v são ortogonais. E a recíproca?
Seja P um ponto interior ao triangulo ABC tal que P A → + P B → + P C → = 0 . Prove que as retas AP, BP e CP são medianas de ABC, logo P é o baricentro desse triângulo.
Dado um triângulo acutângulo ABC no espaço, mostre que é sempre possível escolher os eixos de modo que as coordenadas dos vértices sejam A = (a, 0,0 ), B = (0,b,0) e C (0,0,c)
Seja P : a projeção ortogonal sobre a reta y = 3x. Dado o vetor u = (2, 5), determine x de tal modo que, pondo v = (x, 10), tenha-se Pv = Pu.
Três vetores u, v, w têm o mesmo comprimento e cada um deles forma com o seguinte um ângulo de 120°. Se u = (5, 7), quais são as coordenadas de v e w?