Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 2ª Edição - Alfredo Steinbruch e Paulo Winterle- Ed: 2º - Capítulo 7.5 - Ex. 5
Determinar a equação reduzida referida ao sistema e o gênero da cônica representada pela equação dada a seguir. Esboçar o gráfico.
Passo 1
A questão pede para escrevermos a equação da cônica em um novo sistema de coordenadas em que não aparece o termo misto . Para isso, temos que lembrar que a parte quadrática da equação pode ser escrita como
O que temos que fazer é achar um novo sistema de coordenadas em que a matriz é diagonal. Para isso, temos que achar seus autovalores e autovetores!
Neste caso, a equação é
Olhando apenas para a parte quadrática:
Para achar os autovalores, resolvemos a equação característica:
Assim,
Portanto,
Chegamos então nos autovalores:
Assim, no sistema , teremos
Passo 2
O próximo passo é achar os autovetores associados. Para , temos
Portanto,
Para que ele seja normalizado, escolhemos :
Já para :
Logo,
Escolhendo :
Passo 3
Os autovetores serão as colunas da matriz de mudança de base, de modo que podemos escrever:
Com essas transformações, a equação da cônica é reescrita como
Assim,
Vamos completar quadrados para a parte com :
Assim,
Logo,
Fazendo uma translação:
Assim,
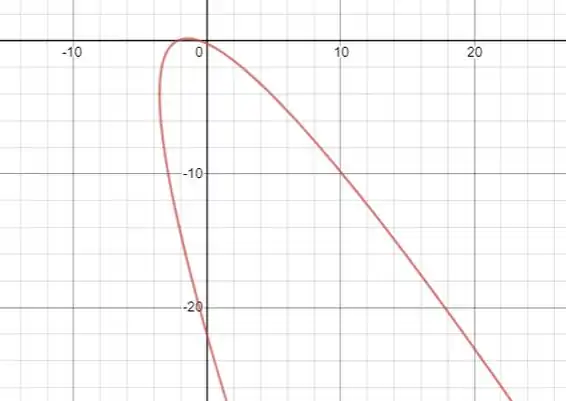
Trata-se de uma parábola, cujo esboço é dado a seguir:
