Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 6.Problemas propostos - Ex. 21

Nos Problemas a, os pares de retas e são paralelas ou concorrentes. Encontrar uma equação geral do plano que as contém.

21)

Passo 1

Fala galera, tudo bem? Vamos resolver junto esse exercício? =D

Para equacionar um plano precisamos de duas coisas: um ponto e um vetor normal , né? E daí a equação geral é:

Sendo assim a ideia pra resolver essa questão é a seguinte: determinar dois pontos de uma reta e um terceiro ponto da outra reta. E daí construir dois vetores, tipo assim:

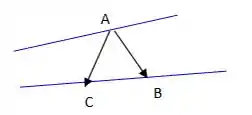
As retas em azul tanto podem ser concorrentes (como no desenho ali em cima) quanto paralelas, vai funcionar do mesmo jeito.

Esses dois vetores vão formar uma base vetorial para nosso plano, sacou? Em seguida vamos fazer o produto vetorial entre eles, pois assim vamos obter um vetor normal aos dois e, consequentemente, ao plano que contém essas duas retas.

Com o vetor normal na mão é só escolher um dos pontos que a gente escreveu antes e equacionar o plano!

Tranquilo? Vamos começar?

Passo 2

Começando pelos pontos. Vou pegar um ponto da reta . Resgatando a equação lá do enunciado temos:

Um ponto simples seria fazer , assim teremos e . Então o ponto é .

Agora vou pegar a reta . Do enunciado temos:

Fazendo temos o ponto e fazendo temos . Com isso podemos escrever os dois vetores:

Passo 3

Agora com os dois vetores o próximo passo é fazer o produto vetorial entre eles:

Passo 4

Agora juntando o vetor normal com o ponto (obs: aqui poderia ser escolhido qualquer um dos três pontos ta? Escolhi esse por simplicidade mesmo =D), podemos escrever uma equação geral pra esse plano: