Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 2.Problemas Propostos - Ex. 15

Determinar o simétrico do ponto P ( 3,1 , - 2 ) em relação ao ponto A ( - 1,0 , - 3 ) .

Passo 1

E aí, tudo bem?

Vamos chamar o simétrico de P ' . Seria tipo isso:

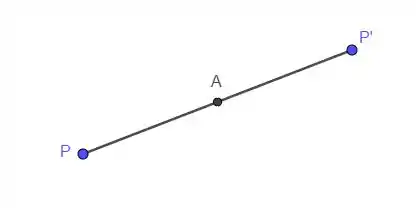
No caso a gente tem o P e o A , queremos achar o P ' .

Repare o seguinte, o ponto A é o ponto médio do segmento P P ' - .

Vamos definir o ponto P ' = ( x , y , z ) e vamos caminhar pra achar esses valores...

Passo 2

Vamos lá, a gente viu que o A é ponto médio, então vamos colocar isso matematicamente:

A = P + P ' 2

- 1,0 , - 3 = 3,1 , - 2 + ( x , y , z ) 2

- 1,0 , - 3 = 3 + x ,   1 + y ,   - 2 + z 2

Vamos igualar as coordenadas agora:

- 1 = 3 + x 2 → 3 + x =   - 2 → x = - 5

0 = 1 + y 2 → 1 + y = 0 → y = - 1

- 3 = - 2 + z 2 →   - 2 + z = - 6 → z =   - 4

Passo 3

E assim achamos as coordenadas do ponto P ' , que é o nosso simétrico procurado:

P ' = ( - 5 , - 1 , - 4 )

E acabamos por aqui😉

Resposta

P ' = ( - 5 , - 1 , - 4 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Figura 1.35 estão representados os vetores coplanares u → , v → e w → . Indicar, na própria figura, os vetoresb) α u → e β w → tal que v → = α u → + β w →
No mesmo sistema cartesiano x O y , representar:os vetores u → = 2 , - 1 e v → = - 2,3 , com origem nos pontos A 1,4 e B 1 , - 4 , respectivamente;
Dados os pontos A 3 , - 4 e B - 1,1 e o vetor v → = - 2,3 , calcular 3 v → - 2 A - B
Sejam os pontos A - 5,1 e B 1,3 . Determinar o vetor v → tal que A = B + 3 v →
Sejam os pontos A - 5,1 e B 1,3 . Determinar o vetor v → tal que B = A + 2 v →