Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 9a
No mesmo sistema cartesiano , representar:
- os vetores e , com origem nos pontos e , respectivamente;
Passo 1
- Vamos lá, temos que o vetor pode ser representado por:
Sabendo que a origem está em , temos então que .
O ponto de extremidade do segmento é então o ponto , vamos então substituir os valores para achar esse ponto:
Pronto, temos que o ponto de extremidade do segmento é .
Passo 2
Vamos agora fazer para o outro vetor, temos que o vetor pode ser representado por:
Sabendo que a origem está em temos então que .
O ponto de extremidade do segmento é então o ponto , vamos então substituir os valores para achar esse ponto:
Pronto, temos que o ponto de extremidade do segmento é .
Passo 3
Agora vamos representar os vetores e :
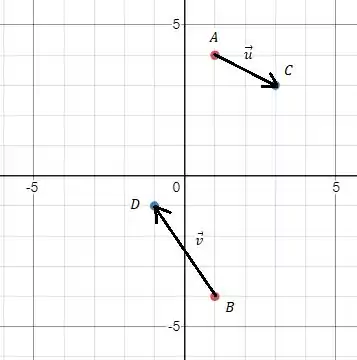
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Dado o triângulo da Figura 5-8, sejam a = | | C B → | | e b = | | C A → | | suponhamos que a ≠ b . Seja Y a intersecção da reta AB com a bissetriz do ângulo externo do vértice C.c) Mostre que Y divide
Dado o triângulo ABC, seja X a interseção do lado AB com a bissetriz do ângulo interno de vértice C (Figura 5-8) e sejam a = | | C B → | | e b = | | C A → | | .Exprima C X → em função de C A → ,C B →
Na Figura 5.9, A M → = 2 M B → e 3 A N → = N C → . Exprima X em função de A, A B → , A C → .
Sejam A, B e C vértices de um triângulo.Prove (algebricamente) que não existe o ponto X quando m +n = 0 . E interprete geometricamente este caso.
Os segmentos AN, BP e CM são dois a dois não paralelos. Dê uma condição necessária e suficiente sobre os vetores A N → , B P → e C M → , que não envolva suas normas, para que exista um triângulo de la