Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.3 - Ex. 18

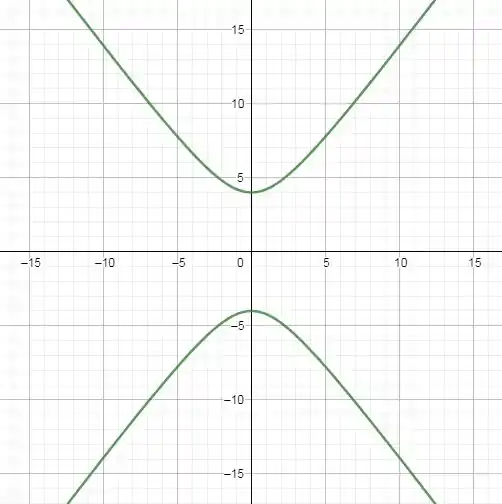
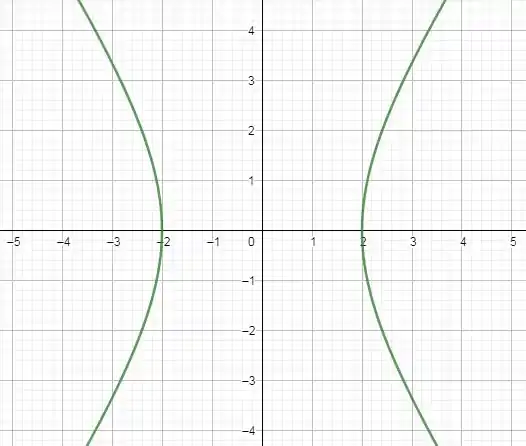
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.

Focos em ( 0,5 ) e ( 0 ,   - 5 ) e um vértice ( 0 ,   4 ) .

Passo 1

Primeiramente vamos achar o centro da hipérbole, para isso basta entendermos que os dois focos estão alinhados com o centro, que por sua vez está no meio dos dois pontos e é equidistante aos focos. Assim podemos calcular o ponto C (centro) como o ponto médio entre o segmento dos dois focos.

x c = 0 + 0 2 ,     y c = 5 + - 5 2

x c = 0 2 ,     y c = 0 2

x c = 0 ,     y c = 0

C   ( 0 ,   0 )

Passo 2

Agora vamos procurar a metade da distância focal c , para isso podemos fazer de duas maneiras. Calculando a distância entre os focos e dividir por 2 ou calcular a distância entre o centro e um dos focos. Abaixo segue o cálculo pelo segundo método.

c 2 = 0 - 0 2 + 0 - 5 2

c 2 = 0 2 + 5 2

c = 5

Passo 3

Agora vamos procurar a para isso vamos calcular a distância entre o centro e o vértice.

a 2 = 0 - 0 2 + 4 - 0 2

a 2 = 0 2 + 4 2

a = 4

Passo 4

Agora vamos aplica a Relação Pitagórica para encontrar b .

c 2 = a 2 + b 2

5 2 = 4 2 + b 2

9 = b 2

b = 3

Passo 5

Agora vamos organizar a fórmula desta hipérbole, como o eixo principal da hipérbole é paralelo ao eixo   y , então   a deverá estar abaixo das coordenadas de   y e o mesmo deverá ser positivo.

y 2 4 2 - x 2 3 2 = 1

y 2 16 - x 2 9 = 1

Resposta

y 2 16 - x 2 9 = 1

Segue a representação gráfica desta hipérbole

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

São dados, graficamente, o eixo transverso A 1 A 2 e os focos ( F 1 e F 2 ) de uma hipérbole. Descreva um método de construção com régua e compasso: de pontos da hipérbole, baseado apenas na Definição
Supondo que a reta t : x - y + 2 = 0 tangencia uma única curva C (elipse ou hipérbole) de focos F 1 e F 2 ,verifique em cada caso se C é elipse ou hipérbole e utilize a propriedade de reflexão para de
Sejam F 1 e F 2 os focos da hipérbole H : x 2 a 2 - y 2 b 2 = 1 , e r 1 e r 2 , as respectivas diretrizes associadas. Seja H ' a hipérbole determinada como na Observação 22-37, tomando-se e = c / a ,
Dados os pontos distintos M e N e um número real não-nulo k , prove que o lugar geométrico dos pontos X tais que sua projeção ortogonal Q sobre a reta M N não pertence ao interior do segmento M N e sa
Resolva o Exercício 22-139 substituindo a elipse pela hipérbole H : x 2 / a 2 - y 2 / b 2 = 1 .