Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.3 - Ex. 35

Ache o volume do sólido gerado pela rotação em torno do eixo x, da região limitada pela hipérbole x 2 a 2 - y 2 b 2 = 1 e pela reta x = 2 a .

Passo 1

Sabendo que a equação da hipérbole é x 2 a 2 - y 2 b 2 = 1   , podemos esboçar o gráfico:

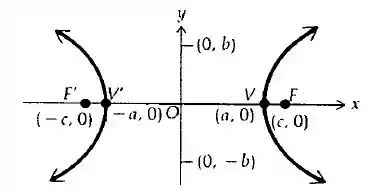
Para calcular o volume de um sólido de revolução devemos usar o conceito de limite. Como a hipérbole vai de x = a até x = 2 a :

V = π ∫ a 2 a f x 2 . d x

Para achar f x isolamos o y na equação da hipérbole:

x 2 a 2 - 1 = y 2 b 2

y ² = b ² x 2 a 2 - b ²

y = ± b ² ( x 2 - a 2 ) a 2

Substituindo na integral:

V = ± π ∫ a 2 a b ² ( x 2 - a 2 ) a 2 2 . d x

V = ± π ∫ a 2 a b ² ( x 2 - a 2 ) a 2 . d x

V = π . b 2 a 2 ∫ a 2 a ( x 2 - a 2 ) . d x

V = π . b 2 a 2 ∫ a 2 a x 2 . d x - ∫ a 2 a a 2 . d x

V = π . b 2 a 2 x 3 3 - a 2 . x | 2 a a

V = π . b 2 a 2 ( 2 a ) 3 - a ³ 3 - a 2 . [ 2 a - a ]

V = π . b 2 a 2 7 a 3 3 - a ³

V = π . b 2 a 2 4 a 3 3

V = 4 π a b 2 3

Resposta

V = 4 π a b 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas.Vértices em ( 5,5 ) e ( 5 , - 1 ) , excentricidade e = 2 .
Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas.Centro C ( 2 , - 3 ) , eixo real paralelo a 0 y , passando por ( 3 , - 1 ) e ( - 1,0 ) .
Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas.Centro C ( - 2 , 1 ) , eixo real paralelo a 0 x , passando por ( 0 , 2 ) e ( - 5,6 ) .
Obter a equação reduzida resultante de uma translação de eixos, classificar, dar os elementos e representar graficamente as equações: x 2 - y 2 - 8 x - 4 y + 11 = 0
Em cada um dos problemas 25 a 30, determinar o centro, os vértices, os focos e a excentricidade das hipérboles dadas. Esboçe o gráfico. 4 x 2 - y 2 - 32 x + 4 y + 24 = 0