Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 130

  1. Determine, em função de a e b , os vértices e a área do quadrado de lados paralelos aos eixos coordenados, inscrito na elipse E : x 2 / a 2 + y 2 / b 2 = 1 .
  2. Mostre que, se os dois lados do quadrado do item (a) contém os focos da elipse, então b é média geométrica entre a e c , e o lado maior do retângulo fundamental é média geométrica sobre a diagonal e o lado menor.

Passo 1

  1. Temos o seguinte esquema, onde A B C D é um quadrado de lado 2 l e F 1 ,   F 2 são os focos da elipse.

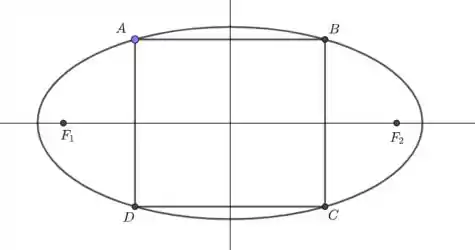
    Sejam A = - l ,   l ,   B = l ,   l ,   C = l ,   - l e D = - l ,   - l . Substituindo as coordenadas de qualquer um desses pontos na equação da elipse, temos

    l 2 a 2 + l 2 b 2 = 1 ∴ l 2 b 2 + a 2 a 2 b 2 = 1 ∴ l 2 = a 2 b 2 a 2 + b 2

    Assim, a área do quadrado será:

    A = 2 l 2 = 4 l 2 ⟹ A = 4 a 2 b 2 a 2 + b 2

    Passo 2

Se F pertence a um dos lados, então o lado do quadrado será igual à distância focal:

2 l = 2 c ∴ l = c ⟹ a b a 2 + b 2 = c

a 2 b 2 = c 2 a 2 + b 2 ∴ b 2 a 2 - c 2 = c 2 a 2

Lembrando que a 2 = b 2 + c 2 ⟹ b 2 = a 2 - c 2 . Assim,

b 2 ⋅ b 2 = c 2 a 2 ∴ b 4 = c 2 a 2 ⟹ b = a c

o que mostra que b é média geométrica de a e c .

Passo 2

Lembrando que o retângulo fundamental é o retângulo de lados 2 a e 2 b , segue que o maior lado é 2 a . A diagonal medirá:

d 2 = 2 a 2 + 2 b 2 = 4 a 2 + b 2 ⟹ d = 2 a 2 + b 2

Do passo anterior, vimos que

a b a 2 + b 2 = c ∴ a 2 + b 2 = a b c = a b b 2 / a = a 2 b ⟹ a 2 + b 2 = a 2 b

pois lembre-se que b = a c ⟹ c = b 2 / a .

Assim, temos que

d = 2 ⋅ a 2 b ∴ 2 a 2 = b d ⟹ 4 a 2 = 2 b d ⟹ 2 a = 2 b ⋅ d

que é o que queríamos demonstrar.

Resposta

Os vértices serão A = - l ,   l ,   B = l ,   l ,   C = l ,   - l e D = - l ,   - l , onde l = a b a 2 + b 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que a órbita de um planeta tenha a forma de uma elipse com eixo maior cujo comprimento é 500 milhões de quilômetros. Se a distância entre os focos for de 400 milhões de quilômetros, ache a equ
A Definição 10.2.1 apresenta um procedimento para fazermos os gráficos de uma elipse. Para aplicar o método a 4 x 2 + 9 y 2 = 36 , determine primeiro os pontos de intersecção com os eixos coordenados.
O teto de um saguão com 10 m de largura tem a forma de uma semi-elipse com 9 m de altura no centro e 6 m de altura das paredes laterais. Ache a altura do teto a 2 m de cada parede.
Percorrendo em sentido inverso as etapas na obtenção da equação 8 a partir da equação 1 , prove que se P x ,y for qualquer ponto cujas coordenadas satisfazem 8 , F P - + F ' P - = 2 a onde F e F ' são
Nos exercícios de 1 a 16, ache o centro, vértices, focos e extremidades do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 4 . 16 x 2 + 9 y 2 = 1 44