Os pontos e são, respectivamente, extremidades do eixo transverso e do eixo conjugado de uma hipérbole de centro , e é um dos focos. é um ponto da hipérbole tal que é perpendicular ao eixo transverso e .
- Exprima em função da excentricidade da hipérbole.
- Mostre que e não são paralelos.
Passo 1
- Temos o seguinte esquema
- Se e fossem paralelos, existiria (com o valor calculado no item (a)) tal que
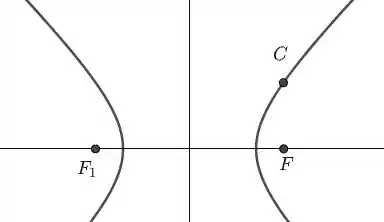
Temos que a abcissa de vale (onde é a distância focal). Logo,
Portanto, .
Passo 2
Temos:
Também,
Portanto,
Passo 3
Assim, teríamos:
o que é impossível!! Assim, e não são paralelos.
Resposta
- Demonstração.