Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.2 - Ex. 38

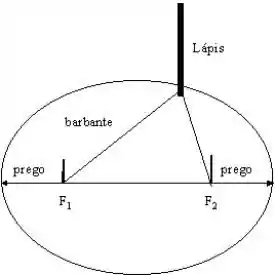
A Definição 10.2.1 apresenta um procedimento para fazermos os gráficos de uma elipse. Para aplicar o método a , determine primeiro os pontos de intersecção com os eixos coordenados. Obtenha os focos sobre o eixo usando um compasso com o centro em um dos pontos de intersecção com o eixo e com raio 3. Aperte então, em cada, foco um percevejo. Pegue um barbante com comprimento 6, que é e prenda as duas extremidades, uma em cada percevejo. Apoie um lápis contra o barbante e estique-o. Movendo o lápis de forma a manter o barbante esticado, trace uma curva. Essa curva é uma elipse, pois o lápis traça o conjunto de pontos do plano cuja soma das distâncias aos percevejos é a constante 6.

Passo 1

Primeiramente vamos passar a equação para a forma reduzida ao dividi-la por 36.

Desta forma temos que o centro é , pois não há termo somando ou subtraindo de e . Além disso e que nos dão os valores dos eixos e .

Passo 2

Para achar os focos tomamos o centro e somamos ou subtraímos da coordenada da qual o eixo principal é paralelo. Neste caso temos que fazer isso em . Assim basta encontrar pela Relação Pitagórica.

Resposta

Tendo os pontos e esticando uma corda num tamanho de pode-se desenhar a elipse. Segue uma imagem mostrando como é o processo de se desenhar a elipse. Nota: usar s seguintes pontos também pode ser úteis .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove, em cada caso, que, se P pertence á região focal de C e Q , não, então P Q intercepta C ( a ) C :x 2 a 2 - y 2 b 2 = 1 ( b ) C :y 2 = 4 p x

Prove que: ( a ) Se P é um ponto interior a elipse E , então qualquer reta que contém P é secante a E ( b ) se s é uma reta disjunta de E , todos os pontos de s são exteriores a E (por essa razão, ret

Prove que uma reta paralela ao eixo de uma parábola tem com ela um único ponto comumProve que, se P pertence a região focal da parábola P , então qualquer reta que contém P e não é paralela ao eixo da

Mostre que qualquer reta que contém o centro da elipse E : x 2 a 2 + y 2 b 2 = 1 é secante a ela, e determine os pontos de interseção em função das coordenadas de um vetor diretor r → = ( m , n ) da r

A elipse da Figura 22 - 23 tem equação x 2 p + y 2 q = 1 ( a ) Desenhe, para cada ponto indicado, o representante do versor de t → = ( p k , - q h) , que tem origem nesse ponto ( b ) Uma partícula des