Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 26.Problemas - Ex. 6

Determine a interseção da esfera x ² + y ² + z ² =   8 com o conjunto C   =   { ( x ,   y ,   z )   ∈   R ³   ;   z   = x 2 + y ²   } . Esboce geometricamente a situação

Passo 1

Saudações galerinha, tudo bem?

Vamos começar a resolver mais um exercício, bora lá então!

Inicialmente temos que encontrar a interseção, para isso vamos comparar os termos:

x 2 + y 2 + z 2 =   8 e z   = x 2 + y ²

Vamos exibir z de outra forma:

Z ² =   x ² +   y ²

Logo:

x 2 + y 2 + x 2 + y ² =   8

2 x 2 + 2 y 2 =   8

Dividindo tudo por 2 :

x 2 + y 2 =   4

Até aí tranquilo?

Passo 2

Com a equação x 2 + y 2 =   4

Vamos obter um circunferência de raio 2 centrada na origem, que será a interseção que procuramos.

Beleza?

Vamos essa situação esboça- lá!

Passo 3

Vamos e esboça essa situação macabra!

Para isso vou utilizar o Geogebra, tranquilo!

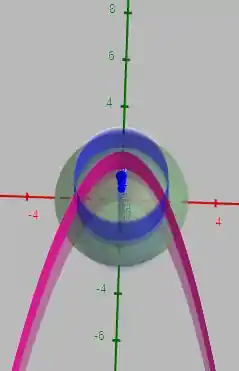
Nosso gráfico ficará assim:

Onde temos:

A interseção x ²   +   y ² =   4 representada em azul

A esfera de equação x 2 + y 2 + z 2 =   8 representada em verde

A parábola z   = x 2 + y ² representada em rosa

Prontinho!

Acabamos te vejo na próxima questão!

Resposta

x 2 + y 2 =   4

Exercícios de Livros Relacionados

Seja O = ( 0,0 , 0 ) . Qual o lugar geométrico dos pontos P = x , y , z tais que O P → 2 = 4 ? Qual figura é representada pela equação x 2 + y 2 = 4 ?
Encontre uma equação em coordenadas cilíndricas da superfície cuja equação em coordenadas cartesianas é dada. d) x 2 + y 2 = z 2
Encontre uma equação em coordenadas cilíndricas da superfície cuja equação em coordenadas cartesianas é dada. c) x 2 - y 2 = 3 z 2
Encontre uma equação em coordenadas cartesianas da superfície cuja equação em coordenadas cilíndricas é dada. c) r 2 c o s ⁡ ( 2 θ ) = z 3
Encontre uma equação em coordenadas esféricas da superfície cuja equação em coordenadas cartesianas é dada. a) x 2 + y 2 + z 2 = 9 z