Seja O = ( 0,0 , 0 ) . Qual o lugar geométrico dos pontos P = x , y , z tais que O P → 2 = 4 ? Qual figura é representada pela equação x 2 + y 2 = 4 ?

O lugar geométrico é uma circunferência de raio 2 , e a figura representada pela equação será um cilindro.

Enunciado

Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 3.2 - Ex. 2

Seja . Qual o lugar geométrico dos pontos tais que ? Qual figura é representada pela equação ?

Passo 1

Primeiro vamos analisar a expressão , temos aqui uma norma ao quadrado, ou seja, o comprimento ao quadrado do vetor sendo igual à , vamos então achar qual é esse comprimento:

Temos então que o comprimento do vetor é de .

Passo 2

Como o ponto está centrado na origem, temos que o lugar geométrico dos pontos com o valor de comprimento significa uma circunferência de raio .

Passo 3

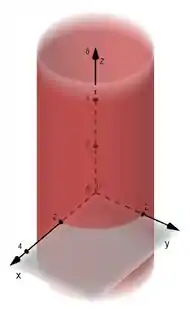
Assim a figura representada pela equação vai ser um cilindro de raio , gerado pelas circunferências obtidas no passo anterior.

Resposta

O lugar geométrico é uma circunferência de raio , e a figura representada pela equação será um cilindro.

Exercícios de Livros Relacionados

A que condições devem obedecer os números a , b e c para que a superfície dada seja uma superfície de rotação em torno de algum dos eixos coordenados? Especifique o eixo de rotação.Elipsóide: x 2 a 2

Completando os quadrados, identifique as superfícies de nível definidas por cada uma das formas quadráticas abaixo: 3 x 2 + y 2 - 2 x y + 2 x z - 2 y z

Mostre que por cada ponto do paraboloide hiperbólico z = x 2 - y 2 passam duas retas inteiramente contidas nele.