Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 6b
6) Determne o vetor nas figuras:
b) 
Passo 1
Primeiramente, vamos analisar a soma dos vetores e . Ela fica assim:
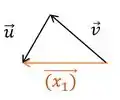
Passo 2
Mas a nossa figura é essa daqui:
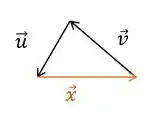
Comparando essas figuras, podemos ver que é o vetor sentido oposto, isso quer dizer que:
E, como , temos que:
Ou
Resposta
Exercícios de Livros Relacionados
Determine uma equação da esfera que passa pela origem e tem centro (1, 2, 3).
Determine uma equação da esfera que passa pelo ponto (4, 3, -1) e tem centro (3, 8, 1).
Sejam A ,B e C pontos quaisquer com A ≠ B . Prove que:c) Um ponto X é um ponto interior ao triângulo A B C ( A ' X → = λ A ' B ' → ,c o m0λ1 , em que A ' é um ponto interior ao segmento A C e B ' é in
Sejam A ,B e C pontos quaisquer com A ≠ B . Prove que:a) Um ponto X pertence a reta determinada por A e B ( A X → = λ A B → ) se, e somente se, C X → = α C A → + β C B → com α + β = 1 .
Sejam A ,B e C pontos quaisquer com A ≠ B . Prove que:b) Um ponto X pertence ao interior do segmento A B ( A X → = λ A B → , com 0λ1 se, e somente se, C X → = α C A → + β C B → , com α0 ,β0 e α + β =