A diagonal de um quadrado está contida em . Sendo um dos vértices, determine os outros três.

O que temos nesse exercício é algo assim:

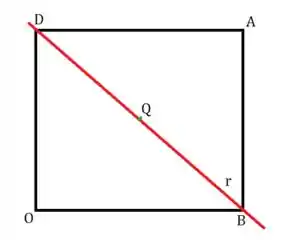
Onde , é o centro do quadrado e .

Vamos começar encontrando o ponto . Ele é um ponto de tal que é perpendicular a , vetor diretor de .

Um ponto genérico de é , então temos . Aí:

Substituindo no ponto , temos que o centro do quadrado está em

Além disso, .

O vértice do quadrado é simétrico a em relação a . Opa, como assim?

O que estamos falando é que , belezinha? Porque como é o centro do quadrado, ele tem a mesma distância até e até , e o vetor é paralelo e tem mesmo módulo que o vetor .

Sendo assim:

Ufa, já achamos um dos vértices hehe agora só falta e :)

Vamos calcular o módulo da diagonal do quadrado, ou seja, o módulo de , pois esse valor vai ser o mesmo de , afinal, as diagonais do quadrado devem ter módulos iguais né? Hehe

Temos , sendo assim:

Portanto, a diagonal do nosso quadrado vale 2 ta ok?

Agora vamos pensar: tem módulo 2, então tanto quanto devem ter metade disso, porque ta no meio entre e .

Logo,

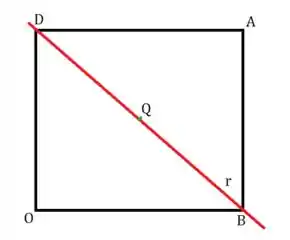
Para encontrarmos e , vamos encontrar os pontos de tais que a distância de até eles seja .

Um ponto genérico de é .

Queremos que , sabendo que :

Então, temos duas possibilidades para , que no caso são os nossos vértices e :

OBS: pode acontecer de e , o que importa é que achamos os outros vértices hahaha :)