Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 19.Exercício - Ex. 16a
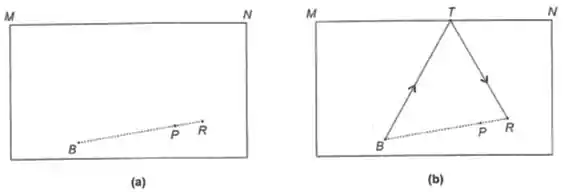
Disputando uma partida de sinuca com seus amigos, Paulinho viu-se diante da situação ilustrada na Figura 19-3 (a), em que o ponto representa a bola branca, ,a preta, e a rosa (esta era a bola da vez). Para sair da sinuca, Paulinho decidiu usar a tabela e acertou a bola rosa sem tocar na preta (Figura 19-3 (b)).
- Supondo que , , e , calcule as coordenadas do ponto .
- Substitua os dados do item (a) por , , e e veja o que acontece.
Passo 1
As imagens da Figura 19-3 são essências para percebemos o que temos que fazer. Temos que descobrir um ponto , que é interno ao segmento , tal que os segmentos e , em relação ao segmento , sejam congruentes.
Em outras palavras, a medida angular entre os vetores e é o mesmo que e . Esta é a relação que precisaremos utilizar.
Mas bom, para podermos chegar ao ponto de usar a relação de medida angular, precisamos determinar alguns pontos antes. Primeiro, vamos determinar a reta que passa por e tem vetor diretor . Ela será:
Portanto, como o ponto é interior a , temos um valor de , sendo e (pois é o lugar de uma caçapa, tal que .
Para finalizar a etapa inicial, vamos calcular os vetores e . Eles são:
Passo 2
Agora que determinamos todos os parâmetros iniciais, vamos descobrir o valor de que satisfaz a questão da congruência dos vetores. Portanto,
Elevando ao quadrado ambos os membros, temos:
Resolvendo a equação do segundo grau acima, vamos obter ou . Como temos a restrição de que e , visto que o ponto é um ponto interior, o valor de que devemos utilizar é .
Sendo assim, as coordenadas do ponto é: