Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 19.Exercício - Ex. 14
Determine as extremidades e de uma das diagonais de um losango contido no plano , sabendo que , e que o ângulo mede .
Passo 1
Seja . Como pertence ao plano , segue que , ou seja:
Vamos usar nosso conhecimento geométrico para terminar de resolver o problema. Ora, sabemos que é um losango, como mostra a figura abaixo.
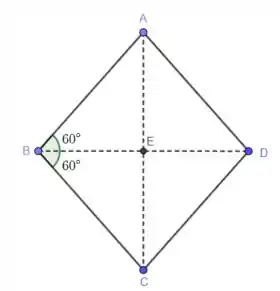
Na figura acima, traçamos as diagonais e, de modo que o ponto é a intersecção dessas diagonais. Note que poderíamos obter o valor de a partir da trigonometria básica do triângulo . Para isso, precisaremos do valor de . Porém, sabemos que uma das características de um losango é que os quatro triângulos são congruentes, de forma que
Agora, vamos calcular a :
Por fim, notemos que
Passo 2
Temos agora três equações e três incógnitas (a saber, ).
- ;
- ;
- .
Vamos, agora, trabalhar as equações ii) e iii).
Para ii):
Para iii):
Passo 3
Tudo que nos resta é resolver o sistema de três equações e três incógnitas:
Subtraindo a segunda equações da terceira, temos:
Usando a primeira equação,
Assim, segue que . Substituindo essa relação, por exemplo, na equação 2 do sistema:
Assim, podemos ter ou . Finalmente, segue que podemos ter ou . Temos, portanto, duas soluções: ou . O que significa encontrarmos dois pontos? Significa que já encontramos e !! Note que se trocarmos as posições de e no desenho, haverá apenas uma mudança no “sentido” que visualizamos o losango.
Resposta
Os pontos são e .