Um hexágono regular está contido em π : x + y + z - 1 = 0 . Sendo A = 1 ,0 ,0 e D = - 1 3 , 2 3 , 2 3 dois vértices diametralmente opostos, determine os outros quatro.

Os vértices são 2 3 ,- 1 3 , 2 3 ,2 3 , 2 3 , - 1 3 ,0,0 , 1 ,0,1 , 0 .

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 19.Exercício - Ex. 08

Um hexágono regular está contido em . Sendo e dois vértices diametralmente opostos, determine os outros quatro.

Passo 1

Veja a figura abaixo

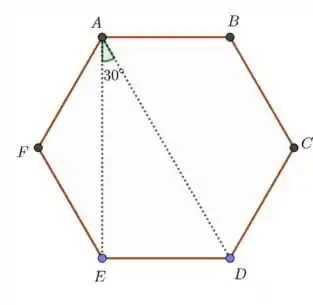
Vamos dizer que .

Vamos calcular :

Portanto, vemos que

O centro do hexágono é o ponto médio do segmento :

Passo 2

Vamos calcular o produto escalar

Além disso, sabemos que , de modo que . Na equação acima, temos

Assim, segue que .

Devemos encontrar uma terceira equação.

Passo 3

Notemos que , já que é um triângulo equilátero. Assim,

Passo 4

Substituindo o valor de , temos

Assim, temos ou . Note, portanto, que já encontramos dois pontos (E e C), dados pelas coordenadas e (veja que os pontos e são obtidos um do outro por uma rotação conveniente do hexágono).

Passo 5

Nos resta encontrar os dois vértices restantes. Para tal, note que:

;
.

Assim, se tomarmos e , teremos:

Resposta

Os vértices são .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar o ângulo entre as seguintes retas:a) r 1 : x = - 2 - t y = t z = 3 - 2 t e r 2 : x 2 = y + 6 1 = z - 1 1 b) r 1 : y = - 2 x + 3 z = x - 2 e r 2 : y = z + 1 - 1 ; x = 4 c) r 1 : x = 1 + 2 t

Determinar o valor de n para que seja de 30 ° o ângulo entre as retasa) r 1 : x - 2 4 = y 5 = z 3 e r 2 : y = n x + 5 z = 2 x - 2 b) r 1 : y = n x - 1 z = 2 x e r 2 : e i x oO y

21. Determinar o ângulo entre as seguintes retas:a) r 1 : x = - 2 - t y = t z = 3 - 2 t e r 2 : x 2 = y + 6 1 = z - 1 1

Disputando uma partida de sinuca com seus amigos, Paulinho viu-se diante da situação ilustrada na Figura 19-3 (a), em que o ponto B representa a bola branca, P ,a preta, e R a rosa (esta era a bola da