Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 9.Problemas - Ex. 1

Qual é a distância da origem à reta 5 x - 2 y = 8 ?

Passo 1

Fala aí pessoal tudo blz?

Nessa questão ele deseja saber qual a distância da origem à reta 5 x - 2 y = 8

Lembrando que para acharmos a distância entre um ponto a uma reta, devemos nos lembrar que,

a x + b y = c a x + b y = c '

b x - a y = 0 b x - a y = 0

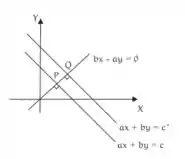
Pode ficar calminho que você vai entender legal, só confia.

Passo 2

Sabendo que,

5 x - 2 y = 8 , temos

Que para determinarmos a distância,

P = ((a c)/(a^2 + b^2) , (b c)/(a^2 + b^2)) e Q = ((a c^')/(a^2 + b^2) , (b c^')/(a^2 + b^2))

P = ((5.8)/(5^2 + ( - 2 )^2) , (- 2.8)/(5^2 + ( - 2 )^2)) e Q = ((5 c^')/(5^2 + ( - 2 )^2) , (- 2 c^')/(5^2 + ( - 2 )^2))

P = ((40)/(29) , (- 16)/(29)) e Q = ((5 c^')/(29) , (- 2 c^')/(29))

Ficando,

d (P , Q) = (5 c^' - ( - 2 c^' ))/(sqrt(((40)/(29))^2 + (- (16)/(29))^2)) = (7 c ')/((8 sqrt(29))/(29)) = (203 c^')/(8 sqrt(29))

Espero ter ajudado, e até a próxima.

Resposta

(203 c^')/(8 sqrt(29))

Exercícios de Livros Relacionados

Achar a distância entre r_1 e r_2 nos casos:r_1 : x = 2 - t y = 3 + t z = 1 - 2 t r_2 : x = t y = - 1 - 3 t z = 2 t
Achar a distância entre r_1 e r_2 nos casos:r_1 : x = 3 y = 4 r_2 : e i x o d o s z
Achar a distância entre r_1 e r_2 nos casos:r_1 : y = 2 x z = 3 r_2 : (x , y , z) = (2 , - 1 , 2) + t . ( 1 , - 1 , 3 )
Achar a distância entre r_1 e r_2 nos casos:r_1 : x = 3 y = 2 r_2 : x = 1 y = 4
6.1.3. Obtenha uma equação do lugar geométrico dos pontos que equidistante das retas:r: (x, y, z) = (0,-1,0) + t (1,0,0) e s: (x, y, z) = (0,1,0) = t (0,0,1). Que lugar Geométrico é esse?