Exercícios de Distância entre Retas - Lista de Exercícios Resolvida

Calcular a distância entre as retas e o eixo dos .

Calcular a distância entre as retas e

Calcular a distância entre as retas que passa pelos pontos e e que passa pelos pontos e

Sendo e . Calcular a distância entre elas.

Calcular a distância entre as retas e

Calcular a distância entre as retas e

Calcular a distância entre as retas e

Calcular a distância entre as retas e

Calcular a distância entre as retas e

Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.

Considere a reta de equação vetorial

E a reta de equação simétrica:

A distância entre as retas e é igual a

a)

b)

c)

d)

e)

Em sejam r a reta que contém o ponto e que é perpendicular ao plano , e s a reta que contém o e de direção . A distância entre r e s vale:

A distância entre as retas

é:

Considere as retas reversas

Se e são os pontos tais que a distância de a seja mínima, então é igual a:

Considere as retas em

e .

(b) Calcule a distância entre as retas e .

(c) Determine a posição relativa entre as retas e .

(d) Determine uma equação paramétrica da reta que liga os dois pontos mais próximos de e , ou seja, a reta com as seguintes propriedades:

(i) ;

(ii) ;

(iii) e são concorrentes;

(iv) e são concorrentes.

Considere as retas e de dadas pelas equações e respectivamente. Considere uma circunferência de centro e raio inscrita entre as duas retas como na figura abaixo.

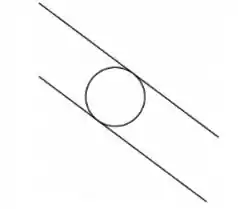
1. Determine todos os pontos que equidistam das retas e
2. Determine o valor de
3. Determine a equação da reta que passa por e é ortogonal às retas e
4. Determine o valor do raio
5. Assuma que o segumento de reta é a projeção ortogonal de em e determine as coordenadas de e de

Dadas as retas e .

a) Estude a posição relativa entre e .

b) Calcule a distância entre e .

Seja , . Ache a distância entre a reta e o eixo . Faça um desenho.

Determine a distância entre as retas abaixo:

b)

Determine a distância entre as retas abaixo:

a)

Sejam e duas retas.

a) Determine para que as retas sejam coplanares (não sejam reversas).

Sejam e duas retas.

b) Para o valor de encontrado determine a posição relativa entre e .

A distância da reta à reta

Sejam e retas distintas em . Considere as seguintes afirmações:

A distância entre e será igual a zero, se e somente se, e forem concorrentes;

se e forem paralelas, então para qualquer ponto , valerá que a distância entre e será igual à distância entre e ;

se e forem reversas, então para qualquer ponto , valerá que a distância entre e será igual à distância entre e .

Assinale a alternativa correta:

a) todas as afirmações são necessariamente verdadeiras;

b) apenas a afirmação é necessariamente verdadeira;

c) apenas as afirmações e são necessariamente verdadeiras;

d) apenas as afirmações e são necessariamente verdadeiras;

e) apenas a afirmação é necessariamente verdadeira.

Considere as retas e .

1. Determine a posição relativa entre as retas e .
2. Calcule a distância entre as retas e .

Considere as retas

e .

Determine os pontos pertencentes à reta que distam da reta .