Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 1.2 - Ex. 38

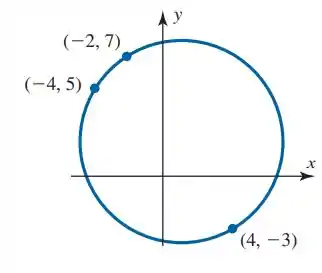
Encontre os coeficientes a ,   b ,   c   e d tais que a curva mostrada seja o gráfico da equação:

a x 2 + a y 2 + b x + c y + d = 0

Passo 1

Primeiramente, vamos “adaptar” a equação da curva dividindo-a por a . Assim, a equação fica:

x 2 + y 2 + b a x + c a y + d a = 0

Passo 2

Agora, trocaremos as variáveis da forma:

b a = B c a = C d a = D

Para reescrever a equação que fica:

x 2 + y 2 + B x + C y + D = 0

Passo 3

Vamos substituir os pontos que satisfazem a equação da curva para obtermos o sistema com seus coeficientes.

- 2 B + 7 C + D = - 53 - 4 B + 5 C + D = - 41 4 B - 3 C + D = - 25

Passo 4

Agora, reescrever o sistema como uma matriz ampliada e escalonar

Para essas operações, utilizaremos o rótulo   L para designar a linha e o operdor:

→ L   q u e   s e r á     a l t e r a d a → O p e r a ç ã o

- 2 - 4 4 7 5 - 3 1 1 1 - 53 - 41 - 2 5 → L 2 → L 2 - L 1 L 3 → L 3 - L 1 - 2 - 2 6 7 - 2 - 10 1 0 0 - 53 12 28

- 2 - 2 6 7 - 2 - 10 1 0 0 - 53 12 28 → L 1 → L 1 - L 2 L 3 → L 3 + 3 L 2 0 - 2 0 9 - 2 1 1 0 0 - 65 12 - 4

0 - 2 0 9 - 2 1 1 0 0 - 65 12 - 4 → L 1 → L 1 - 9 L 3 L 2 → L 2 + 2 L 3 0 - 2 0 0 0 1 1 0 0 - 29 4 - 4

Passo 5

0 - 2 0 0 0 1 1 0 0 - 29 4 - 4 → L 2 → - 1 2 L 2 0 1 0 0 0 1 1 0 0 - 29 - 2 - 4

Passo 6

Agora, reescrecer a matriz   0 1 0 0 0 1 1 0 0 - 29 - 2 - 4 como o sistema linear

B = - 2 C = - 4 D = - 29

Repassando para as os coeficientes anteriores:

B = b a = - 2     ∴     b = - 2 a C = c a = - 4   ∴     c = - 4 a     D = d a = - 29   ∴     b = - 2 9 a

Resposta

b = - 2 a c = - 4 a     b = - 29 a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove que: a) Toda matriz é equivalente por linhas a ela mesma (reflexividade);
Encontre condições sobre os b i ' s para que cada um dos sistemas seja consistente (isto é, tenha solução):a) x 1 - 2 x 2 + 5 x 3 = b 1 4 x 1 - 5 x 2 + 8 x 3 = b 2 - 3 x 1 + 3 x 2 - 3 x 3 = b 3
Para cada sistema linear dado, encontre todos os valores de a para os quais o sistema não tem solução, tem solução única e tem infinitas soluções:b) x + y + z = 2 2 x + 3 y + 2 z = 5 2 x + 3 y + a 2 -
Determine os coeficientes a , b , ced da função polinomial p x = a x 3 + b x 2 + c x + d , cujo gráfico passa pelos pontos P 1 = 0,10 , P 2 = 1,7 , P 3 = 3 , - 11 eP 4 = ( 4 , - 14 ) .
Determine os coeficientes a , b , ced do círculo, x 2 + y 2 + a x + b y + c = 0 , que passa pelos pontos pelos pontos P 1 = - 2 , 7 , P 2 = - 4 , 5eP 3 = 4 , - 3 .