Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 7.4 - Ex. 9
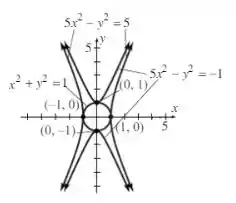
Esboce o círculo unitário e as curvas de nível correspondentes à forma quadrática dada. Mostre que o círculo unitário intersecta cada uma dessas curvas em exatamente dois pontos e verifique que os extremos condicionados ocorrem nesses pontos.
Passo 1
No exercício 1 encontramos os valores de máximo e mínimo de :
Máximo condicionado é e ocorre quando Mínimo condicionado é e ocorre quando .
Passo 2
Geometricamente, isso significa que a curva = (relacionada ao nosso máximo condicionado) deveria apenas tocar o círculo unitário nos pontos ;Já a curva =(relacionada ao nosso mínimo condicionado) deveria apenas tocar o círculo unitário no ponto .
Passo 3
Finalmente temos esse desenho aí:
Resposta
Exercícios de Livros Relacionados
Encontre uma mudança de variáveis ortogonal que elimine os termos mistos da forma quadrática Q e expresse Q em termos das novas variáveis. Q = 3 x 1 2 + 4 x 2 2 + 5 x 3 2 + 4 x 1 x 2 - 4 x 2 x 3
Em cada caso, encontre uma mudança de variável ortogonal que elimine o termo misto da forma quadrática e expresse a forma quadrática em termos das variáveis novas. a - 3 x 1 2 + 5 x 2 2 + 5 x 1 x 2 b
Sejam A uma matriz simétrica n × n e q x = x T A x Onde x é um vetor qualquer em R n expresso em forma de coluna. O que pode ser dito sobre o valor de q se x for um autovetor unitário associado a um a
Suponha que a matriz hessiana de uma certa forma quadrática f x , y seja dada por H = 2 4 4 2 O que pode ser dito sobre a localização e a classificação dos pontos críticos de f?
Encontre, se houver, todos os pontos críticos de f e classifique-os como máximos relativos, mínimos relativos ou pontos de sela. f x , y = x 3 + y 3 - 3 x - 3 y