Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 1m
Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade.
Passo 1
De cara isso não parece nenhuma cônica que conhecemos, podemos afirmar que isso não é nenhuma das cônicas que estudamos até agora. Porém se isolarmos dessa forma:
E tirarmos as raízes de ambos os lados:
Teremos um par de retas! Duas retas que passam pela origem de inclinação :
Passo 2
Plotando essas duas retas, temos:
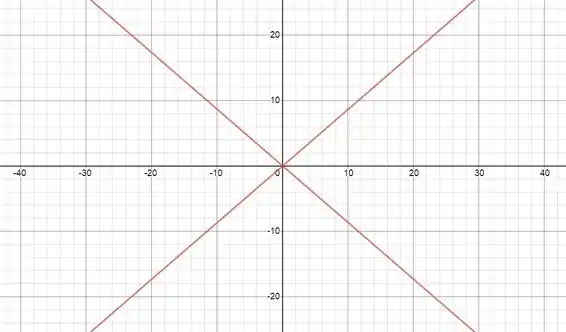
Passo 3
Os conceitos de excentricidade, diretriz e foco não se aplicam a essa figura, já que não temos uma cônica “de verdade”.
Resposta
Exercícios de Livros Relacionados
Determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Focos F ± 3,0 e equações das assíntotas y = ± x
Determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.Focos F 1 - 6,1 e F 2 0,1 e eixo real medindo 4
Determinar os focos da hipérbole de equações x = 4 + 5 tan θ e y = - 5 + 2 sec θ
Determinar uma equação da curva descrita por um ponto que se move, de modo que sua distância ao ponto A ( - 1 ,3 ) seja:Igual a sua distância à reta x = 3 ;
Encontrar uma equação da hipérbole de excentricidade2 e foco coincidentes com os focos da elipse x 2 25 + y 2 9 = 1 .