Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.3 - Ex. 26

Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.

Um foco em - 3 - 3 13 ,   1 , as assíntotas interceptam-se em - 3 ,   1 e uma assíntota passa pelo ponto 1 ,   7 .

Passo 1

As assíntotas apenas se interceptam no centro da hipérbole assim temos C   ( - 3 ,   1 ) . Agora vamos calcular o coeficiente angular de uma das assíntotas através de seus dois.

m = Δ y Δ x = - 3 - 1 1 - 7 = 4 6 = 2 3

Passo 2

Agora vamos procurar c para isso vamos calcular a distância entre o centro e um dos focos.

c 2 = - 3 - 3 13 - - 3 2 + 1 - 1 2

c 2 = 13 2 + 0 2

c = 3 13

Passo 3

A fórmula para se encontrar a assíntota é y - h = ± b a ( x - k ) . Assim temos que o coeficiente angular da assíntota nos dá a   e   b e podemos identificar a = 3 k e b = 2 k , uma vez que k representa um número em comum desta divisão. Agora usando a Identidade Pitagórica podemos encontrar k e consequentemente a e b .

c 2 = a 2 + b 2

3 13 2 = ( 3 k ) 2 + 2 k 2

9 ∙ 13 = 9 k 2 + 4 k 2

9 ∙ 13 = 13 k 2

9 = k 2

3 = k

a = 9 e b = 6

Passo 4

Agora vamos organizar a fórmula desta hipérbole, como o eixo principal da hipérbole é paralelo ao eixo   x , então   a deverá estar abaixo das coordenadas de   x e o mesmo deverá ser positivo.

x + 3 2 9 2 - y - 1 2 6 2 = 1

x + 3 2 81 - y - 1 2 36 = 1

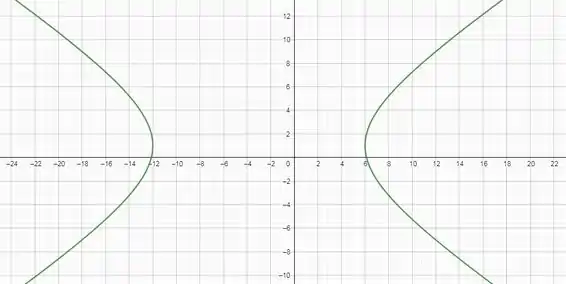
Resposta

x + 3 2 81 - y - 1 2 36 = 1

Segue a representação gráfica desta hipérbole

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

( a ) O paralelogramo A B C D tem os lados A B e D C paralelos ao eixo transverso da hipérbole H : x 2 3 - y 2 2 = 1 e os lados A D e B C contidos em retas tangentes a H . Os pontos de tangência têm c
Sejam H : x 2 a 2 - y 2 b 2 = 1 , θ um número do intervalo [ 0 , π [ , α = a 2 s e n 2 θ - b 2 cos 2 ⁡ θ , e u → = ( cos ⁡ θ , s e nθ ) . ( a ) Prove que, se α0 , qualquer reta r paralela a u → é seca
Sejam P e Q pontos distintos, pertencentes a uma hipérbole H . Prove que as retas tangentes a H em P e Q são paralelas se, e somente se, o centro da hipérbole é o ponto médio de P Q .
Sejam H uma elipse e u → um vetor não nulo, Prove que: ( a ) os pontos médios das cordas de H paralelas a u → pertencem a uma reta que contém o centro; ( b ) se P Q é uma corda paralela a u → que cont
Os vértices do paralelogramo A B C D pertencem as assíntotas da hipérbole H : x 2 - 4 y 2 + 7 = 0 e um de seus lados mede 73 e está contido em uma reta tangente a H . Determine A , B , C , D .