Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.3 - Ex. 19

Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.

Centro na origem, focos sobre o eixo   y e passando pelos pontos ( - 2 ,   4 ) e ( - 6 ,   7 ) .

Passo 1

Pelos dados do enunciado entendemos que a hipérbole tem a seguinte forma

y 2 a 2 - x 2   b 2 = 1

Passo 2

Vamos aplicar os valores dos pontos na hipérbole

Para ( - 2 ,   4 )

4 2 a 2 - ( - 2 ) 2   b 2 = 1

16 a 2 - 4   b 2 = 1

Multiplicando tudo por a 2 b 2

b 2 16 - 4 a 2 = a 2 b 2 (1)

Para ( - 6 ,   7 )

7 a 2 - ( - 6 ) 2   b 2 = 1

49 a 2 - 36   b 2 = 1

Multiplicando tudo por a 2 b 2

b 2 49 - 36 a 2 = a 2 b 2 (2)

Passo 3

Para achar a 2 e b 2 vamos resolver os sistemas.

Multiplicando (1) por -9 e somando à (2) temos

b 2 49 - 36 a 2 - b 2 16 ∙ 9 + 36 a 2 = - 9 a 2 b 2 + a 2 b 2

b 2 49 - b 2 16 ∙ 9 = - 8 a 2 b 2

b 2 49 - 144 = - 8 a 2 b 2

95 = 8 a 2

95 8 = a 2

Agora aplicando a 2 em (1)

b 2 16 - 4 95 8 = 95 8 b 2

- 95 2 = 95 8 b 2 - b 2 16

- 95 2 = b 2 95 8 - 16

- 95 2 = b 2 - 33 8

- 95 2 - 8 33 = b 2

b 2 = 380 33

Passo 4

Tendo a 2 e b 2 basta substituir na hipérbole.

y 2 95 8 - x 2   380 33 = 1

8 y 2 95 - 33 x 2   380 = 1

Resposta

8 y 2 95 - 33 x 2   380 = 1

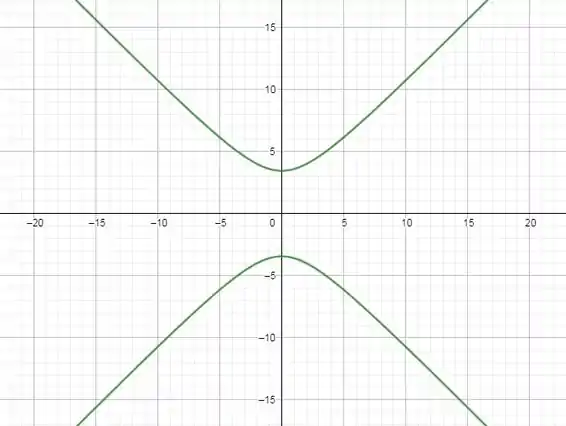
Segue a representação gráfica desta hipérbole

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A reta t : x - y + 2 = 0 tangencia uma hipérbole de focos F 1 = ( 1,1 ) e F 2 = ( 0,3 ) . Determine o ponto de tangência e os parâmetros geométricos da hipérbole.
Prove que qualquer reta tangente a uma hipérbole separa os focos.
Caso t seja tangente a alguma hipérbole H de focos F 1 e F 2 , obtenha uma equação de H . ( a ) F 1 = - 2 2 , 0F 2 = 2 2 , 0 t : 3 x - 5 y - 4 = 0 ( b ) F 1 = 0 , - 4F 2 = 0 , 4 t : 2 x + y + 2 = 0 (
Sejam T = ( h , k ) um ponto da hipérbole H : x 2 a 2 - y 2 b 2 = 1 e A e B os pontos em que a reta tangente a hipérbole em T intercepta as assíntotas. ( a ) Escreva as coordenadas de A e B em termos
Obtenha equações das retas que contém o ponto P = ( 1 , - 9 ) e são tangentes a hipérbole de equação 3 x 2 - y 2 = 39 . Determine os pontos de tangência e a reta normal em cada um deles.