Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 5.6 - Ex. 29
Um espelho plano está apoiado em uma parede vertical formando um ângulo de com ela. Se um feixe de luz de raios paralelos for emitido verticalmente (do teto para o chão), determine a direção dos raios refletidos.
Passo 1
Pra resolver essa questão, vamos dar uma olhadinha na geometria da questão. A gente tem que saber aquele pouquinho de física também hahahah. Quando o raio de luz bate no espelho, ele reflete com o mesmo ângulo com o espelho, assim ó:
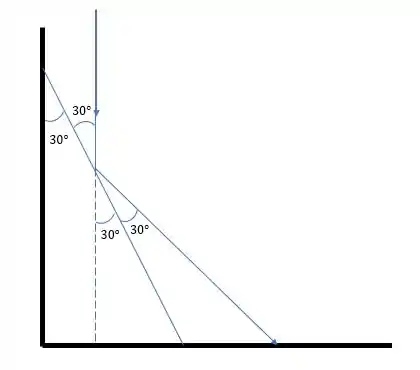
Passo 2
Então se liga, inicialmente o raio estava vindo na vertical pra baixo, e aí sua direção é:
E depois, como vimos ali no desenho, ele sai formando com a vertical, andando pra direita e para baixo. Então a sua nova direção é:
Então fechou!
Resposta
Exercícios de Livros Relacionados
Qual é a aplicação A que representa uma contração de 1 2 seguida por uma rotação horária de 45 ° ?
Dê quando possível, exemplos de transformações lineares T , S , L , MeH satisfazendo: T : R 3 → R 2 , sobrejetora. S : R 3 → R 2 , com ker S = 0,0 , 0 L : R 3 → R 2 , com I mL = 0,0 M : R 2 → R 2 ,
Sejam α = 0,2 , ( 2 , - 1 ) e β = 1,1 , 0 , 0,0 , - 1 , 1,0 , 1 bases de R 2 e R 3 . S β α = 2 4 00 0 - 4 Dê a expressão para S ( x , y ) .
Determine quais das seguintes funções são aplicações lineares: f : R 2 → R 2 ( x , y ) → x + y , x - y g : R 2 → R ( x , y ) → x y h : M 2 → R a cb d → det a cb d k : P 2 → P 3 a x 2 + b x + c → a x
Qual é a transformação linear T : R 2 → R 3 tal que T 1,1 = ( 3,2 , 1 ) e T 0 , - 2 = 0,1 , 0 ?Ache T ( 1,0 ) e T ( 0,1 ) .Qual é a transformação linear S : R 3 → R 2 tal que S 3,2 , 1 = ( 1,1 ) , S 0