Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 5.Problemas Propostos - Ex. 58
Estabelecer as equações simétricas da reta que passa pelo ponto intercepta o eixo e é paralela ao plano.
Passo 1
Precisamos encontrar a equação da reta que é paralela ao plano que atinja o eixo . Isso significa que a reta passa por algum ponto em , mas que não toca os outros eixos (e) e que passe também por um ponto .
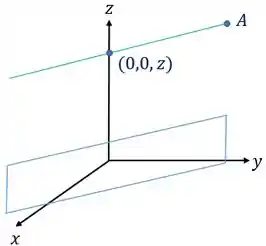
Precisamos de um ponto dela e seu vetor diretor, essa reta tem um ponto que passa em que chamaremos de E o vetor pode ser o segmento de reta , que é dado por:
Como a reta é paralela ao plano, o vetor diretor deve ser perpendicular ao vetor normal ao plano, que pode ser dado utilizando os termos que contem e do próprio plano:
Passo 2
Agora, temos que garantir a condição de perpendicularidade dos vetores, onde o produto escalar entre eles é nulo (lembrando de uma regrinha que diz que o produto escalar entre dois vetores sempre nos dará um número).
Então, o vetor diretor é dado por:
A metade desse vetor também é um vetor diretor, e vamos usá-la para facilitar nossos cálculos:
Passo 3
Nós temos um vetor diretor da reta e um ponto , com isso conseguimos estabelecer as equações simétricas da reta, que são dadas por:
Vamos considerar os termos e os pontos do vetor e os termos os termos do vetor diretor.