Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 5.Problemas Propostos - Ex. 55
Nos problemas 55 e 56, determinar a equação geral do plano que contém o ponto e a reta e interseção dos planos e :
Passo 1
Nós temos dois planos que talvez se interceptem em uma reta. Precisamos fazer duas coisas, a primeira é pegar dois pontos que estejam na interseção entre os dois planos e a outra é enconrar um terceiro plano que contenha essa reta e um ponto qualquer fora dele.
Vamos fazer isso montando um sistema com os dois planos:
Com isso, podemos dizer que:
Substituindo na primeira equação, teremos:
Dessa forma, nossos conjuntos de pontos terão a forma
Passo 2
Como sabemos como o sistema se comporta, temos a liberdade para escolher valores para e calcular . Por conveniência escolhemos múltiplos de para facilitar a divisão do termo .
Inicialmente, quando :
Nosso primeiro ponto .
O segundo ponto, quando :
Nosso segundo ponto será .
Passo 3
Agora, queremos encontrar a equação do plano que passe pelos pontos e :
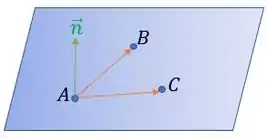
Para isso, precisamos achar o vetor normal ao plano, então, precisamos encontrar os segmentos e .
Tendo os pontos , , .
O segmento é dado por , e o segmento :
Por fim, faremos o produto vetorial entre esses dois vetores:
Isso significa que nossa equação pode ser dada por:
Substituindo o ponto na equação, teremos:
A equação será: