Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 11.Exercício - Ex. 20a
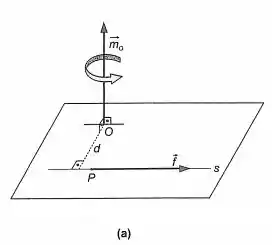
Na Estática dos Sólidos, é importante levar em conta o ponto de aplicação de uma força. Se é o sistema formado pelas forças . Fixado o ponto (pólo), o momento de em relação a é o vetor . Se está em equilíbrio, e. Para os intens (a), (b) e (c), formado por uma única força , aplicada em P, e a reta por P, paralela a (Figura 11-7 (a)).
(a) Prove que, se então .
Passo 1
Para essa questão é importante que vocês tenham alguma noção sobre Estática dos Sólidos, beleza?
Queremos provar que se então .
Vamos traduzir isso?
Queremos provar que se o segmento da reta que une dois pontos diferentes de aplicação do torque é paralelo à reta suporte da força , o momento gerado pela força nesses pontos é de mesma intensidade , ok?
Então, vamos lá!
Passo 2
O torque é definido pela distância entre a reta suporte da força perpendicular ao braço vezes a intensidade da força. Portanto, se o segmento de reta definido pelos pontos e é paralelo a
, o braço da força em relação a esses pontos são iguais, logo, o torque terá a mesma intensidade.
Desse modo, provamos o que a questão nos pedia 😉.
Resposta
Ei, a resposta está no passo a passo :)