Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 11.Exercício - Ex. 20b
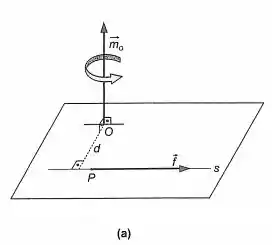
Na Estática dos Sólidos, é importante levar em conta o ponto de aplicação de uma força. Se é o sistema formado pelas forças . Fixado o ponto (pólo), o momento de em relação a é o vetor . Se está em equilíbrio, e. Para os intens (a), (b) e (c), formado por uma única força , aplicada em P, e a reta por P, paralela a (Figura 11-7 (a)).
(b) Se , seja . Prove que .
Passo 1
Para essa questão é importante que vocês tenham alguma noção sobre Estática dos Sólidos, beleza?
Queremos provar que Se , seja . Prove que .
Vamos traduzir isso?
Queremos provar que o momento de uma força não perpendicular a seu braço é igual ao produto vetorial da força menos a projeção sobre o seu braço e o próprio braço de aplicação.
Então, vamos lá!
Passo 2
Para a gente calcular o torque de uma força, inicialmente devemos decompô-la em duas componentes: uma perpendicular ao seu braço, e outra paralela, beleza?
Passo 3
Agora, temos dois torques para serem calculados: o da projeção (paralela ao braço) e o da forma menos a projeção (perpendicular ao braço).
Calculando os torques, temos:
Portanto, provamos que . 😉
Resposta
Ei, a resposta está no passo a passo :)