Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 11.Exercício - Ex. 44

Sejam uma base ortonormal positiva e uma operação interna em que satisfaz as propriedades

Supondo que

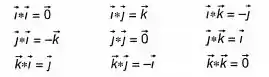
prove que , isto é , quaisquer que sejam e .

Passo 1

Bora lá!

Para começarmos a resolução vamos ver o que a questão nos dá, beleza?

É dada uma operação interna que satisfaz as seguintes propriedades:

E ainda, que para os vetores da base canônica, temos os seguintes resultados:

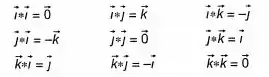
Passo 2

Se nós observarmos os resultados obtidos para a base canônica, percebemos que de fato a operação apresenta os mesmos resultados do produto vetorial. Mas só isso não basta, vamos provar de maneira algébrica que as relações são válidas para qualquer vetor?

Passo 3

Tomando os vetores como:

Substituindo nas propriedades da operação interna, temos:

Ufa! Chega de contas.

Qual é a conclusão que podemos tirar?

Se liguem, como para as bases ortonormais a operação definida é um produto vetorial e as demais propriedades do problemas são válidas para o produto vetorial, pode concluir que existe uma identidade entre as operações, que é exatamente o que queríamos provar 😉.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam B= ( a → , b → , c → ) uma base de V , u →=( x , y , z ) B . Que condições devem satisfazer x , y e z para que ( a →+u → , b →+u → , c →+u → ) sejam também uma base de V ?

ABCD é um paralelogramo, | a | →= 2 e | b | →= 3 . Determine o coseno do menor ângulo formado pelas diagonais do paralelogramo.(Sugestão: A C →= a → +b → ; D B →=. . . )

Dados os vetores u → , v → , w → e t → tais que u →∧v →= w →∧t → e u →∧w →= v →∧t → , prove que u → -t → e v → -w → são vetores l.d..

Verdadeiro ou falso?Se verdadeiro, demonstre, se falso, dê contra-exemplo:se a →+b → +c →=0 , então a →∧b →= b →∧c → = c→∧a → ;se a →∧b →= b →∧a → , então a → e b → são paralelos; a →∧b →= a →∧c → imp

Dados os vetores u →=( 2,2 , 4 ) e v →=( 1,1 , 0 ) , determine uma base ortonormal positiva tal que seu primeiro vetor seja paralelo a u → e seu segundo vetor seja uma combinação linear de u → e v → .