Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 3.1 - Ex. 1d
Nos exercícios 1-2, desenhe um sistema de coordenadas (como na Figura 3.1.10) e marque, em cada parte, o ponto cujas coordenadas são dadas.
- (a) (3,4,-5)
Passo 1
Vamos desenhar um plano cartesiano e marcar as coordenadas. E com elas formar um paralelepípedo.
O vetor deve ser desenhado partindo da origem até chegar no vértice oposto do paralelepidpedo.
O desenho deve ficar parecido com isso:
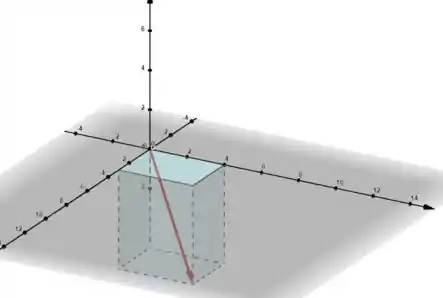
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Sejam u =( - 2 ,6 ,2,1 ) , v =( - 3 ,0 ,8,0 ) ew=( 9 ,1 , - 6 , - 6 ) .Calculead i s t â n c i ae n t r e- 3 uev +5 w â .
Considere os pontos P ( 3 ,- 1 ,4 ) ,Q ( 6 ,0 ,2 )eR ( 5 ,1 ,1 ) . Encontre o ponto S em R 3 cujo primeiro componente seja - 1 e tal que P Q → seja paralelo a R S → .
Sejam u =( - 2 ,6 ,2,1 ) , v =( - 3 ,0 ,8,0 ) ew=( 9 ,1 , - 6 , - 6 ) .Calculep r o j wu .
Considere os pontos P ( - 3 ,1 ,0 ,6 ) ,Q ( 0 ,5 ,1 ,- 2 )eR ( - 4 ,1 ,4 ,0 ) . Encontre o ponto S em R 4 cujo terceiro componente seja 6 e tal que P Q → seja paralelo a R S → .
Determine se o conjunto de vetores dado é ortogonal. Se for, normalize cada vetor para formar um conjunto ortonormal. u = - 2 ,0 ,1 ,v = 1 ,1 ,2 ,w = ( 1 ,- 5 ,2 )