Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 1k
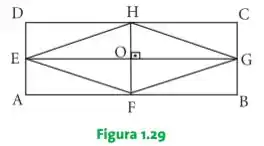
1. A figura 1.29 apresenta o losango inscrito no retângulo , sendo o ponto de intersecção das diagonais desse losango. Decidir se é verdadeira ou falsa cada uma das seguintes afirmações:
k)
Passo 1
Então pessoal, antes de respondermos a nossa questão vamos nos lembrar sobre qual o significado dessa notação, tudo bem? Nos foi dado o seguinte:
Essas duas barras querem dizer que os vetores em questão são paralelos, galera! Mas pera, o que são vetores paralelos mesmo? São vetores que possuem mesma DIREÇÃO, tudo bem? Note que o sentido e o tamanho não nos importa, apenas a direção dos vetores. Um exemplo de vetores paralelos:
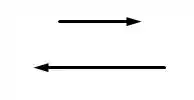
Note que eles possuem sentidos e tamanhos diferentes, mas a direção é a mesma, e é nisso que vamos focar, beleza? Show!
Passo 2
Se traçarmos os vetores em questão na figura que nos foi dada, teremos:
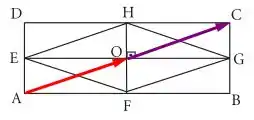
No qual o vetor em vermelho é e o vetor em roxo é . Podemos notar que os vetores possuem tamanhos idênticos, uma vez que o retângulo é uma figura simétrica, além de possuírem sentidos idênticos também! Além disso, repare que a direção dos vetores também é idêntica, galera! Em termos da rosa dos ventos, ambos os vetores estão numa direção Sudoeste-Noroeste. Sendo assim, podemos concluir que a afirmação é verdadeira.
Resposta
A afirmação é verdadeira.