Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 11a
Na Figura 1.35 estão representados os vetores coplanares , e . Indicar, na própria figura, os vetores
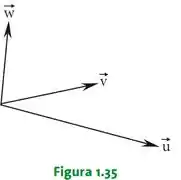
- e tal que
Passo 1
Nesse caso como o vetor está para baixo e para a direita, precisaremos que
Já que o sentido do vetor é o mesmo que o de (para a direita) e o sentido do vetor é oposto de , no qual aponta para cima e aponta para baixo, por isso precisamos inverter o sentido de
Passo 2
Agora que sabemos como são os vetores, só nos resta soma-los:
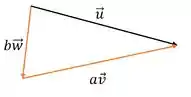
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Dado o triângulo da Figura 5-8, sejam a = | | C B → | | e b = | | C A → | | suponhamos que a ≠ b . Seja Y a intersecção da reta AB com a bissetriz do ângulo externo do vértice C.d) O que ocorreria se
Sejam A, B e C vértices de um triângulo.Relacione o caso particular em que m +n = 1 com o Exercício 5.4.
Dado o triângulo ABC não retângulo, a = t g ,  b = t gB ^ e c = t gC ^ .Prove que no ortocentro é interior ao triângulo se, e somente se, ele for acutângulo. (No caso em que o triângulo é retângulo,
Dado o triângulo ABC, seja X a interseção do lado AB com a bissetriz do ângulo interno de vértice C (Figura 5-8) e sejam a = | | C B → | | e b = | | C A → | | .Mostre que X divide (A, B) na razão b a
Dado o triângulo da Figura 5-8, sejam a = | | C B → | | e b = | | C A → | | suponhamos que a ≠ b . Seja Y a intersecção da reta AB com a bissetriz do ângulo externo do vértice C.b) Exprima C Y → em fu