Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 29
A figura 1.65 apresenta um paralelepípedo retângulo de arestas paralelas aos eixos coordenados e de medidas . Determinar as coordenadas dos vértices deste sólido, sabendo que .
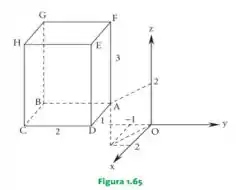
Passo 1
Então galera, para determinarmos as coordenadas dos outros vértices deste sólido devemos utilizar da nossa noção de perspectiva, uma vez que a figura é , ok? Show! Vamos discutir cada ponto separadamente, a fim de facilitar nossa visualização dos pontos. O primeiro ponto já nos foi dado, que é:
Para o ponto :
Eixo – O ponto está na mesma reta que o ponto , então a coordenada vale também;
Eixo – Da origem até o ponto temos que . Ademais, de até temos que , então somando esses valores teremos que a coordenada vale ;
Eixo – A altura do ponto é a mesma altura do ponto , então a coordenada vale também. Conclusão:
Vamos fazer essa análise para os outros pontos agora. Let’s go!
Passo 2
Para o ponto :
Eixo – Da origem até o ponto temos que . Ademais, de acordo com a figura, de até (apenas no eixo ), temos que . Somando esses valores teremos que a coordenada vale ;
Eixo – Da origem até o ponto temos que . Ademais, de até (apenas no eixo ) temos que , então somando esses valores teremos que a coordenada vale ;
Eixo – A altura do ponto é a mesma altura que o ponto e , logo, temos que a coordenada vale também. Conclusão:
Para o ponto :
Eixo – Da origem até o ponto temos que . Ademais, de acordo com a figura, de até (apenas no eixo ), temos que . Somando esses valores teremos que a coordenada vale ;
Eixo – Como o ponto está na mesma reta que o ponto no eixo , então temos que a coordenada vale também;
Eixo – A altura do ponto é a mesma altura que o ponto e , logo, temos que a coordenada vale também. Conclusão:
Para o ponto :
Eixo – Da origem até o ponto temos que . Ademais, de acordo com a figura, de até (apenas no eixo ), temos que . Aqui estamos comparando o ponto com o porque eles estão na mesma linha em . Somando esses valores teremos que a coordenada vale ;
Eixo – Como o ponto está na mesma reta que o ponto no eixo , então temos que a coordenada vale também;
Eixo – Da origem até o ponto temos que . Do ponto até a altura que o ponto se encontra temos unidades. Sendo assim, a coordenada vale . Conclusão:
Passo 3
Para o ponto :
Eixo – O ponto está na mesma reta que o ponto , então a coordenada vale também;
Eixo – Como o ponto está na mesma reta que o ponto no eixo , então temos que a coordenada vale também;
Eixo – Da origem até o ponto temos que . Do ponto até a altura que o ponto se encontra temos unidades. Sendo assim, a coordenada vale . Conclusão:
Para o ponto :
Eixo – O ponto está na mesma reta que o ponto , então a coordenada vale também;
Eixo – Da origem até o ponto temos que . Ademais, de até temos que , então somando esses valores teremos que a coordenada vale ;
Eixo – Da origem até o ponto temos que . Do ponto até a altura que o ponto se encontra temos unidades. Sendo assim, a coordenada vale . Conclusão:
Para o ponto :
Eixo – Da origem até o ponto temos que . Ademais, de acordo com a figura, de até (apenas no eixo ), temos que . Aqui estamos comparando o ponto com o porque eles estão na mesma linha em . Somando esses valores teremos que a coordenada vale ;
Eixo – Da origem até o ponto temos que . Ademais, de até temos que , então somando esses valores teremos que a coordenada vale ;
Eixo – Da origem até o ponto temos que . Do ponto até a altura que o ponto se encontra temos unidades. Sendo assim, a coordenada vale . Conclusão:
E essas são nossas coordenadas, pessoal!
Resposta
Coordenadas dos vértices do sólido:
; ; ; ;
; ; e