A figura dada mostra um sistema de coordenadas retangulares determinado pelos vetores unitários e da base canônica e um sistema de coordenadas determinado pelos vetores unitários e de uma outra base. Encontre as coordenadas dos pontos cujas coordenas estão dadas
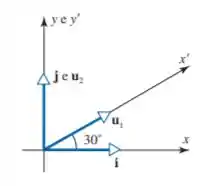
Passo 1
Para o sistema de coordenadas dado vamos montar o seguinte triângulo

A partir do triângulo acima podemos, usando as relações trigonométricas, chegar no seguinte
Passo 2
Portanto, agora ficou simples de achar a correspondência entre qualquer ponto de para . Sendo assim, para teremos
Já para vamos ter
Procedendo da mesma forma vamos encontrar para o terceiro ponto
Por fim, para o nosso último ponto obteremos