Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 13.Exercício - Ex. 14
Mostre que os pontos , , e são vértices de um paralelogramo.
Passo 1
Devemos mostrar que os pontos , , e são vértices de um paralelogramo. Para isso, vamos achar primeiro alguns vetores:
É fácil perceber que não é paralelo a . Portanto, é LI.
Passo 2
Além disso, podemos ver que
Fazendo um desenho:
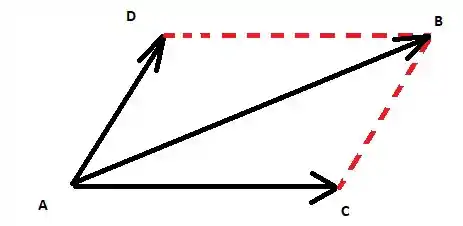
Vemos que se trata de um paralelogramo com diagonais e .
Resposta
Demonstração.
Exercícios de Livros Relacionados
Determine se a expressão faz sentido matemático.b) u .( v + w)
Determine se a expressão faz sentido matemático.c) ( u .v )
Determine se a expressão faz sentido matemático. u .( v . w)
Sejam B = i → , j → uma base ortonormal de V π , P um ponto qualquer de π , u → = m , n B e v → = p , q B vetores LI de V π . Mostre que a área do paralelogramo de vértices P , P + u → ,P + v → e P +
Seja π : 2 x + y - z - 5 = 0 ∑ 1 . Escreva as equações da translação de ∑ 1 para um ponto O 2 do eixo O 1 z de tal modo que qualquer equação geral de π em relação ao novo sistema tenha termo independe