Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 13.Exercício - Ex. 17
Sejam , e pontos quaisquer. Examine se são verdadeiras ou falsas as afirmações seguintes. Justifique sua resposta e interprete geometricamente.
a) Se o determinante formado pelas coordenadas de , e é nulo, isto é,
então , e são colineares.
b) Se , e são colineares, então .
Passo 1
Esse exercício é bem interessante para discutir algumas noções de “ida e volta” em matemática!
Já vou dar a resposta logo de cara e em seguida justificar cada caso: a afirmativa (a) é falsa, mas a (b) é verdadeira. Sei que parece estranho uma ser verdadeira e a outra falsa, já que elas parecem dizer a mesma coisa, mas cuidado: elas não dizem a mesma coisa!
A afirmativa (a) diz que
Já a afirmativa (b) diz que
O que significa a afirmativa (b) ser falsa: se soubermos que os três pontos são colineares e calcularmos o determinante, vamos obter . Mas o fato da afirmativa (a) ser falsa diz que a recíproca não é verdadeira: se o determinante for zero, não significa que necessariamente os pontos serão colineares, eles podem não ser. Vou dar um contra exemplo para mostrar isso:
Calculando o determinante:
Mas e são LI, de modo que os pontos são não colineares. Assim, temos um caso em que mas os pontos não são colineares.
O que nós sabemos com certeza é que se os pontos fossem colineares, o determinante seria nulo, mas ele pode ser nulo mesmo que os pontos não sejam colineares!
Passo 2
Agora vamos demonstrar que o item (b) é verdadeiro. Para isso, vamos considerar a origem . Se os pontos , e são colineares, então os pontos , , e estão num mesmo plano:
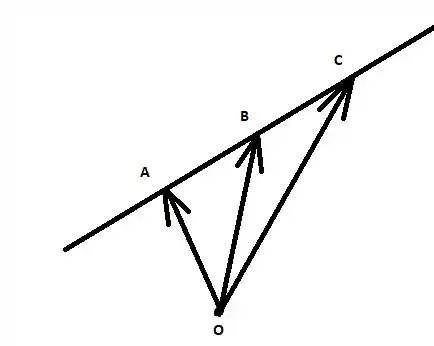
Assim, o conjunto é LD. Portanto, o determinante das coordenadas desses vetores deve ser nulo:
Assim,