Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 3.2 - Ex. 22

Se ‖ v ‖ = 2 e w = 3 , quais são os maiores e menores valores possíveis de ‖ v - w ‖ ? Interprete seu resultado geometricamente.

Passo 1

Fala aê! Tudo certo? Nesta questão precisamos verificar os valores de uma expressão algébrica e representá-la geometricamente. Então vamos lá?!

Primeiro, vamos supor um espaço vetorial. Nesse espaço, dado dois vetores v → e w → , temos um triangulo com lados: v → ,   w → e v → - w → . Nesse triangulo, sabemos que o comprimento de seus lados são os módulos ‖ v ‖ ,     w e ‖ v - w ‖ . Na figura a seguir é possível visualizar o que foi dito.

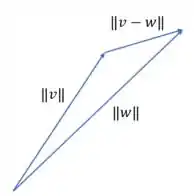
Desigualdades triangulares e desigualdades triangulares inversas são desigualdades fundamentais estendem a espaços vetoriais normatizados propriedades simples de triângulos: dado um triângulo com os lados ‖ v ‖ ,     w e ‖ v - w ‖ , onde qualquer lado é menor que a soma dos outros dois.

No espaço vetorial normatizado, uma das propriedades definidoras da norma é a desigualdade do triângulo. Logo, para ‖ v ‖ = 2 e w = 3 temos:

v - w ≤ v + w ≤ 5

v - w ≥ | v - w | ≥ 1

1 ≤ ‖ v - w ‖ ≤ 5

Portanto, o valor mínimo é 1 e o máximo é 5 .

Resposta

O valor mínimo é 1 e o máximo é 5 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja π : 2 x + y - z - 5 = 0 ∑ 1 . Escreva as equações da translação de ∑ 1 para um ponto O 2 do eixo O 1 z de tal modo que qualquer equação geral de π em relação ao novo sistema tenha termo independe
Dadas equações do conjunto Ω em relação a um dos sistemas de coordenadas ∑ 1 =O 1 , e 1 → , e 2 → , e 3 → e ∑ 2 = ( O 2 , f 1 → , f 2 → , f 3 → ) , obtenha equações de Ω em relação ao outro e identifi
Seja ∑ 2 o sistema obtido pela translação do sistema ortogonal ∑ 1 para um ponto O 2 pertencente a reta r : X = 1,0 , 1 + λ 1,4 , 2 ∑ 1 . Determine, em cada caso, as coordenadas de O 2 em relação a ∑
∑ 1 = O 1 , e 1 → , e 2 → , e 3 → e ∑ 2 = O 2 , f 1 → , f 2 → , f 3 → são dois sistemas de coordenadas tais que O 2 = 1,1 , 1 ∑ 1 e a matriz de mudança de base E = e 1 → , e 2 → , e 3 → para a base F
Adote o enfoque da observação anterior para escrever equações paramétricas de E 3 em relação ao sistema novo.