Seja N=( 0 ,0 ,1 ) o polo norte da esfera unitária S 2={ ( x ,y ,z )∈R ³;x ²+y ²+z ² =1 } ³ ² ² ² . Para cada ponto P=( x ,y ,z ) diferente de N em S2 (isto é, c o mz ≠1 ), seja P'=( x',y ',0 ) o ponto em que a semi-reta NP intersecta o plano Π x y . Use as equações paramétricas de NP para obter as coordenadas x'ey' em função de x ,yez .

X 2 x ’ 2 +y ' 2 y 2 +z 2 = 1 Equivalente ao ponto (1,1) da esfera

Enunciado

Saudações galerinha, tudo bem?

Vamos começar a resolver mais um exercício, bora lá então!

Começaremos visualizando essa situação um pouco estranha, o gráfico abaixo demostra o que se passa neste exercício.

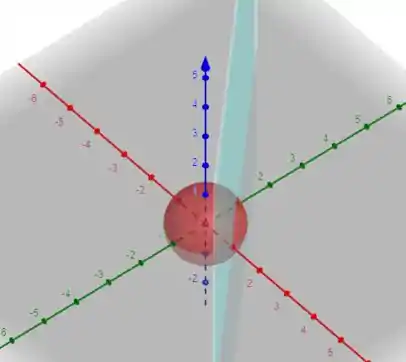
Temos uma esfera sendo cortada por um plano, que na figura está representado com a cor azul claro.

A questão que os pontos desta interseção.

Bora lá começar então!

Dada a equação:

Temos nossa interseção escrita como:

Que é o ponto de nossa esfera.

Prontinho!

Acabamos te vejo na próxima questão!

Equivalente ao ponto (1,1) da esfera